Can a variable have a significant effect on an effect that is non-significant itself?

Question

Let's say I estimate

$d_t = b + \epsilon_t$,

where $d$ stands for some difference between two variables and $b$ is a constant. I estimate this model $i$ times for $i$ different subjects (say firms, individuals, etc.). Put differently, I simply estimate the mean of the differences of two variables for $i$ subjects. Let's say $b$ turns out to be insignificant for every $i$.

I then estimate

$b_i = \gamma_0 + \gamma_1 x_i + \epsilon_t$,

where $b_i$ is the estimation of $b$ for every $i$, $\gamma_0$ is a constant and $\gamma_1$ is the coefficient of some predictor $x_i$.

Can, $\gamma_1$ be significant, eventhough the constants $b_i$ are insignicant themselves? If so, how would you interpret such a significant influence in a meaningful way?

Answer 1

The example below might help to intuitively understand it. It shows a plot of datapoints $d$ (black dots) and the estimates $\hat{b}$ of the population means (blue squares) with the error bars relating to the standard error of the $\hat{b}$. Also shown is a (red) line indicating the linear model for the estimates $\hat{b}$ as a function of the $x$.

So we see that all those individual estimates have each not much accuracy and their difference from zero is not significant.

However because there are so many measurements for the different values of $x$ we can still see a reasonable certain relationship for the $\hat{b}$ as function of $x$.

In order to determine the significance of the linear relationship a lot more data is combined together. That is why you can get the significant relationship for the line b ~ x, but each of the individual points is not significant.

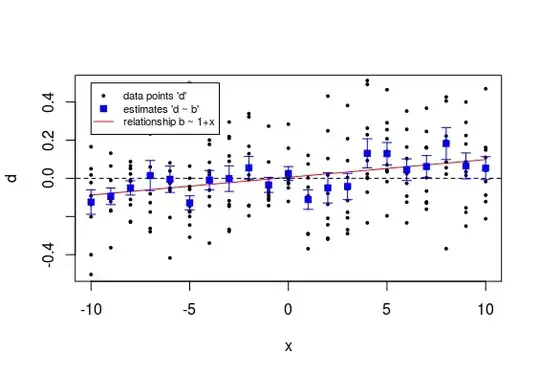
This situation also occurs often when people compare two curves. Some researcher may have taken multiple measurements for each value $x$ and based on a pointwise overlap of error bars the conclusion might be that there is no difference. However, for a linear curve, or some other curve (which takes all the data into account together) the power of a test for differences is much higher. This is why I do not so often focus on making triplicate measurements. When you know the underlying model well then you do not need to take multiple measurements at every single vale of the independent variable $x$, that is because you are not comparing the single points but instead the estimates for the model coefficients.

Code for the graph

Steps:

1. Use an independent variable $x$ with values $-10, -9, -8, \dots, 9, 10$
2. Model unknown variable $b$ according to: $$b \sim N(0.01 x, 0.01^2)$$
3. Model dependent variable $d$ according to $$d \sim N(b, 0.2^2)$$
4. Compute estimates $\hat{b}$ (and determine their significance, which only turns out significant here for the point at x=-5, with p-value 0.006) and perform regression for $\hat{b}$ as function of $x$ (which turns out significant with p-value <0.001

--

set.seed(1)
ns <- 10

# create data
x <- seq(-10,10,1)
b <- rnorm(length(x),mean = 0.01*x,sd = 0.01)
d <- matrix(rep(b,ns),ns, byrow = 1)+rnorm(ns*length(x),0,0.2)
b_est <- colMeans(d)

# blank plot
plot(-100,-100, xlim = c(-10,10), ylim = c(-0.5,0.5), 
     xlab = "x", ylab = "d")

## model for b ~ x
mod <- lm(colMeans(d) ~ x)
summary(mod)
lines(x, predict(mod), col = 2)

# line for reference
lines(c(-20,20), c(0,0), lty = 2)

# add points
for (i in 1:length(x)) {
  # raw data 'd'
  points(rep(x[i],ns),d[,i],pch = 21, col = 1, bg = 1, cex = 0.4)

  # significance of 'b'
  mt <- t.test(d[,i])
  if (mt$p.value < 0.05) {
    text(x[i],0.5,"*",col=2)
  }

  # estimates 'b'
  mod <- lm(d[,i] ~ 1)
  points(x[i],mod$coefficients[1],
         pch = 22, col = 4, bg = 4)

  # error bars
  err <- summary(mod)$coef[2]
  mea <- summary(mod)$coef[1]
  arrows(x[i], mea+err, x[i], mea-err, length=0.05, angle=90, col=4, code = 3)
}

legend(-10,0.5, c("data points 'd'",
                  "estimates 'd ~ b'",
                  "relationship b ~ 1+x"),
       col = c(1,4,2), pt.bg =c(1,4,2),lty = c(NA,NA,1), pch = c(21,22,NA), pt.cex = c(0.4,1,1),
       cex = 0.7)

Answer 2

Yes this is very well possible. It means that the $b$'s have barely an effect on the $d$'s. But there's no reason that this makes that you can not model the $b$'s with some $x$'s.

• This happens clearly when $b$ and $d$ are completely unrelated. E.g. say $d$ is the degree that somebody likes blue more than red, $b$ is somebody's cholesterol level, and $x$ is somebody's saturated fat consumption.

  It is not unimaginable that in some experiment/measurement $x$ (fat consumption) will have a significant effect on $b$ (cholesterol level) in a linear model. But $b$ is not significantly related with $d$ preference for colour.

• The same thing happens also when $b$ and $d$ are likely related (ie. not like the earlier contrived example with clearly unrelated things). For instance $d$ could be some health outcome, like the risk of getting coronary hearth disease.

  In health research (and I am sure other fields have this as well) it happens quite often that some behaviorial parameter $x$ like (eating habits, exercise, etc.) has a significant (measurable) effect on some physiological parameter $b$ (like cholesterol level, body fat percentage, bone strength, etc), but the effect $b$ (and $x$ as well) on some health outcome $d$ (like risk of disease, disability or death) is not so clear and often does not turn into a significant effect in some measurement/experiment.

---

Some more particular (more extreme) case is when $x$ is found to strongly correlate with each of $b$ and $d$, but $b$ and $d$ do correlate a lot with each other.

This is possible. For given correlations among three variables $\sigma$, $\tau$, and $\rho$, there is a range of values that $\rho$ can take (within some bounds) depending on the other two correlations.

$$\sigma\tau - \sqrt{(1-\sigma^2)(1-\tau^2)} \le \rho \le \sigma\tau + \sqrt{(1-\sigma^2)(1-\tau^2)}$$

So this can make that for some data the effect of $x$ in a linear relation is significant for both $b$ and $d$, but still $b$ is not a significant effect in a linear relation for $d$. (In this case, when some weak correlation is present, then it might be the case that more measurements, a larger sample, will show a significant effect)