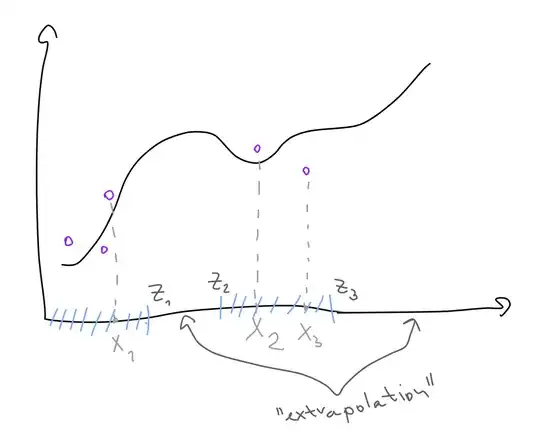
Extrapolation is often defined as predicting the value of an unknown function outside the range of available points. Let's say we are training on $x_1, .., x_n$, $x_{max} = \text{max}(x_i)$, $x_{min} = \text{min}(x_i)$, $d(x_i, x_j)$ is a distance function.
I would take "outside" to mean "far enough away from all training points", $$d(x_{new}, x_i) > K\ \ \forall x_i$$ rather than. literally, "not between $x_{min}$ and $x_{max}$", $$(x_{new} > x_{max}) \lor (x_{new} < x_{min})$$
Not least because the latter makes even less sense for high-dimensional spaces. But even for $\mathbb{R}$, I wouldn't think that, in the general case, for any given $\delta$, it's easier to predict for some $x_i + \delta$ than it is for $x_{max} + \delta$. Is that accurate? If not, why does being "between" matter?. Perhaps it's relevant here than in time series evaluation, it is customary to opt for only evaluating on "future" datapoints, rather than any points that lie far away from training points - mathematically, why is that?
I attached an illustration. $z_1, z_2, z_3$ are "limit" points of "trustworthiness", I would think anything beyond them should be considered extrapolation. If my thinking here is correct, I'd appreciate pointers to any work that develops criteria for such limit points, given a dataset and an algorithm. If not, I'd appreciate any perspective on what I'm missing.