How does one calculate the probabilities of 2 outcomes that are negatively correlated (A happens and B happens, A happens and B doesn't happen, B happens and A doesn't happen, neither A or B happen)?
How does one calculate the probability of 2 outcomes that are negatively correlated?
I believe using the formula below, you can calculate the probability of 2 outcomes that are positively correlated (is this formula correct?), but I am not sure how to translate this to work with a negative correlation value:
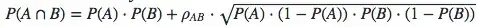
I assume these all use the formula below and you simply plugin in the different P(A) and P(B) values. Please correct me if that is wrong.
The formula doesn't seem to work with these values though (trying to solve for neither A or B occuring): A = 0.1 | B = 0.1 | Corr: -.72
When ever a = .1 and b=.1 and the correlation value is -.72, the formula above produces -0.0548, which doesn't seem right since the probability can't be negative, can it?
Assuming the correlation is 0, the probability should be, 0.01. With a negative correlation, wouldn't it be lower than 0.01? and with a positive correlation, it would be higher than 0.01?
Here is my python code being used: a * b + corr * math.sqrt(a * (1 - a) * b * (1 - b))