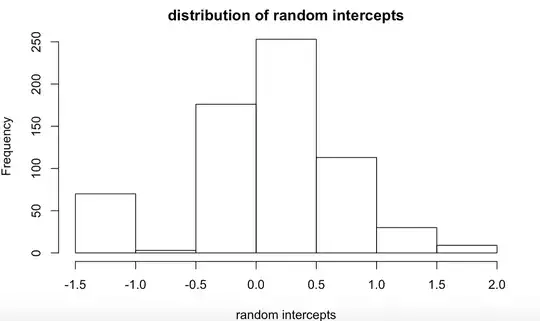
My model gives me random intercepts in which the distribution looks like:
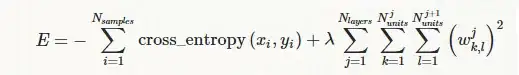
The model is as follows:
mod <- lmer(response ~ 0 + item + (1|id), family = binomial)
Is this still a valid random effects distribution or does this indicate that there's something wrong with my model ?
Edit: this is the distribution of the random intercept of the model above. It was extracted using ranef() in R. This is what it looks like in the bigger picture.
When I increase the bin size, it looks like this:
Edit2: This model is an Item Response (IRT) model (or Rasch) Basically I have a list of patients and their answers to several survey questions. The answers of this survey are binary (e.g. do you exercise at least once a week, etc)
This then transformed into item-response format (wide: patient_id, Q1, Q2, ...Qn to long: patient_id, item (which is Q1,..,Qn) and response (which is the answers to the item column)
Then I fit this data into IRT above, extract the random intercepts as an indices to measure their health level (sort of)