Product of 2 Uniform random variables is greater than a constant with convolution

Question

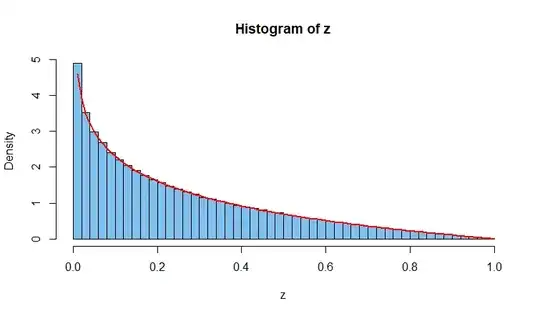
I am trying to formulate the following question. X and Y are IID , uniform r.v. with ~U(0,1)

What is the probability of P( XY > 0.5) = ?

0.5 is a constant here and can be different.

I do respect the geometrical solutions but what i would like to see and understand is the generic approach since X and Y can be other distributions. Specificially solutions through Z = X.Y substition, joint distribution/convolution.

I tried the following conversion. Z = XY and dX = dZ/Y

then

$$ P(Z>0.5) = \int_{0.5}^1 \! f(z/y,y) \, \mathrm{d}y \mathrm{d}{z/y}. $$ $$ = \int_{0.5}^1 \! \int_{0}^{z} \! fy(y)fx(z)\, \mathrm{d}y \mathrm{d}{z/y}. $$ since fy(y) and fx(z) is 1 and 1/z s integral is ln(y) it simplifies to $$ = \int_{0.5}^1 \! ln(z) fx(z)\, \mathrm{d}z. $$

which i am not sure about the correct formulation especially the boundries.

--Edit The standard double integral solution over X and Y is as follows. f(x,y)dydx = f(x)f(y)dy dx since they are IID.

$$ = \int_{0.5}^1 \! \int_{0.5/x}^{x} \! fy(y)fx(x)\, \mathrm{d}y \mathrm{d}{x}. $$ $$ = (1-ln(2))/2 $$ $$ ~=0.15342 $$

The solution through Z=X.Y is K.A. Buhr's to the bottom:

Answer 1

Some hints: Geometrical approaches are much easier for uniform RVs, but the general approach is to integrate the joint PDF in the region that satisfy $XY>\alpha$. The integral will basically look like below:

$$\mathbb P(XY>\alpha)=\iint_{xy>\alpha} f_{X,Y}(x,y)dydx$$

The actual boundaries of the integrals will change with respect to your support.

Answer 2

Multiple answers and partial answers here, some for the more general problem of multiplying $n$ independent standard uniform random variables.

For $n = 2,$ the PDF of the product $Z = XY$ is $f(z) = -\log(z),$ for $0 < z < 1,$ which I believe agrees with @gunes' answer (+1) for the product of two standard uniform random variables.

The following simulation gives a histogram in agreement with this PDF. The red superimposed curve shows this density function.

set.seed(2020)
x = runif(10^6);  y = runif(10^6)
z = x*y
summary(z)
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
0.00000 0.06793 0.18690 0.25011 0.38269 0.99907 

hist(z, prob=T, br=40, col="skyblue2")
curve(-log(x), add=T, col="red", lwd=2)

The CDF is $F_Z(z) = P(Z \le z) = z - z\log(z),$ for $0 < z < 1.$ So $F_Z(.5) = 0.8466$ is the requested probability.

z = .5;  z - z*log(z)
[1] 0.8465736

An empirical CDF (ECDF), based on the million simulated values of $Z$ is shown below as a thin black line. The dashed red line is $F_Z(z)$ as given above. The match is essentially perfect within the resolution of the plot.

plot(ecdf(z))
 curve(x - x*log(x), add=T, col="red", lwd=3, lty="dashed")
 abline(v = .5, col= "blue", lty = "dotted")
 abline(h = 0.8455, col="blue", lty="dotted")

Answer 3

There's really not much point in doing a change of variables here because it doesn't really buy you anything (even if you were doing it for non-uniform RVs).

But, if you insist, if you are trying to evaluate the integral: $$P(XY>\alpha) = \int_0^1\left(\int_0^1 f(x,y) I(xy>\alpha) dy\right)dx$$ you can't directly apply the substitution $x=z/y$ to the outer integral. You need to exchange the integrals first: $$= \int_0^1\left(\int_{x=0}^{x=1} f(x,y) I(xy>\alpha) dx\right)dy$$

Now, we can apply the substitution $x=z/y$, $dx=dz/dy$ and limits $z=0$ to $z=y$ to the inner integral: $$= \int_0^1\left(\int_{z=0}^{z=y} f(z/y,y) I(z>\alpha) \frac{dz}y\right)dy$$ Combining the integration limits and the indicator is difficult. We need to consider the cases where $y$ is less than and greater than $\alpha$ separately: \begin{align} &= \int_0^\alpha\left(\int_{z=0}^{z=y} f(z/y,y) I(z>\alpha) \frac{dz}y\right)dy + \int_\alpha^1\left(\int_{z=0}^{z=y} f(z/y,y) I(z>\alpha) \frac{dz}y\right)dy\\ &= 0 + \int_\alpha^1\left(\int_{z=\alpha}^{z=y} f(z/y,y) \frac{dz}y\right)dy \end{align} Note that in the case of the left integral, where $0\leq y \leq \alpha$, we also have $z \leq y \leq \alpha$, so the indicator is always zero, so that whole integral is 0. In the case of the right integral, we have $y > \alpha$, so for the inner integral $\int_{z=0}^{z=y}$, the indicator is zero for $0 \leq z \leq \alpha$ and one for $\alpha \leq z \leq y$, so that gives us our final limits.

Now, knowing that $f(z/y,y)=1$ over the limits of integration, we can write: $$=\int_\alpha^1\left(\int_{z=\alpha}^{z=y}\frac{dz}y\right)dy$$ and I imagine you can finish it off to get the result $1-\alpha+\alpha \log \alpha$, which was already more or less given in another answer.

Answer 4

You might indeed try some coordinate transforms. E.g. instead of integrating $$\int \int f(x,y) I(xy>a) dx dy$$ you could transform to other variables and integrate $$\int \int g(w,z) I(z>a) dw dz $$

In which case the indicator function is easier to evaluate.

The transform

Say you use $w = y$ and $z = xy$. The distribution function can be computed using the Jacobian

$$J(w,z) = \frac{dx}{dw}\frac{dy}{dz} - \frac{dx}{dz}\frac{dy}{dw} = - \frac{1}{w}$$

and

$$g(w,z) = f(x(w,z),y(w,z) )|J(w,z)| = \frac{1}{w}$$

Integration and domain

For the integration we need to take care that the domain is

$$0 \leq z \leq 1 \quad \text{and} \quad z \leq w \leq 1$$

And the domains for each coordinate are not independent.

Now the integration becomes (the indicator function is gone now and you see it back in the formula as the lower limit for the integration with $dz$)

$$\int_a^1 \int_{z}^1 \frac{1}{w} dw dz $$

The inner term is $$ \int_{1/z}^1 \frac{1}{w} dw = \log(w) \big|_{z}^1 = - \log(z)$$

and you get

$$P(z > a) = \int_{a}^1 - \log(z) dz = z - z\log(z) \big|_{a}^1 = 1 - a + a \log(a)$$

---

Note that if you differentiate the expression that we used you get

$$f(Z=a)= \partial_z P(Z\leq a) = \partial_z \int_{-\infty}^a \int g(w,z) dw dz = \int g(w,z) dw $$

And this is the way how people often compute the pdf $\int |y^{-1}| f(z/y,y) dy$

So using a coordinate transform is not so uncommon to compute a product distribution.