Suppose $X_i \stackrel{i.i.d}{\sim}$ Exp$(1/\theta)$ which implies $\sum_{i =1}^{n} X_i \sim$ Gamma $(n, 1/\theta)$.
But, then, the book that I am reading says that $(2/\theta)\sum_{i =1}^{n} X_i \sim$ Gamma$(n, 2)=$$\chi^2(2n)$. I don't understand how this is true. Can someone please explain this step? Thanks!
I'll let you use moment generating functions or other methods to prove that $X_i \stackrel{iid}{\sim}\mathsf{Exp}(\mathrm{rate}=1/\theta)$ implies $T = \sum_{i=1}^n X_i \sim \mathsf{Gamma}(\mathrm{shape}=n, \mathrm{rate} = 1/\theta).$
For $n=5, \theta=10, \lambda = 1/\theta = 0.1,$ the following simulation in R verifies that this 'works' for a specific case. Recall that $E(T) = n\theta = n/\lambda = 50.$
n = 5; lam = 0.1
set.seed(517)
t = replicate(10^5, sum(rexp(n, lam)))
mean(t)
[1] 49.99174 # aprx 50
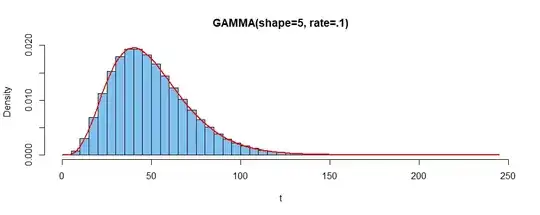
hist(t, prob=T, br=50, col="skyblue2", main="GAMMA(shape=5, rate=.1)")
curve(dgamma(x, n, lam), add=T, col="red", lwd=2)
Also, continuing from above you can show that $Y = 2T/\theta = 2\lambda T \sim \mathsf{Chisq}(\nu=2n).$ Recall that $E(Y) = \nu = 10.$
y = 2*lam*t
mean(y)
[1] 9.998347 # aprx 10
hist(y, prob=T, br=50, col="skyblue2", main="CHISQ(10)")
curve(dchisq(x, 2*n), add=T, col="red", lwd=2)
More generally, $\mathsf{Chisq}(\nu) \equiv \mathsf{Gamma}(\mathrm{shape} = \nu/2, \mathrm{rate} = 1/2)$ $\equiv \mathsf{Gamma}(\mathrm{shape} = \nu/2, \mathrm{scale} = 2).$
