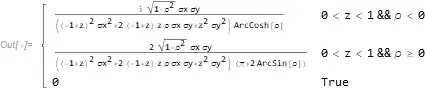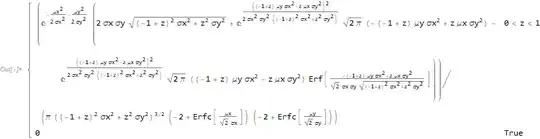What is the expected value of $\frac{X}{X+Y}$ when $X,Y > 0$?

Question

I've read this question (and suggested links) which poses the same question assuming $X,Y$ are bivariate standard normal. Since the support includes $0$, the expectation does not exist. This makes perfect sense.

I'm interested instead in the situation where $X,Y$ are still normally distributed, but bounded away from zero (say the support is truncated at some $\delta>0$). They possess different means and variance, however. If it helps, $X,Y$ are independent, though I'm curious about any insight to the general case.

Answer 1

If $X$ and $Y$ are positive random variables both with finite means, then $\frac{X}{X+Y} \in (0,1)$ and so $E\left[\frac{X}{X+Y}\right] \in (0,1)$ also. Similarly, $\frac{Y}{X+Y} \in (0,1)$ and so $E\left[\frac{Y}{X+Y}\right] \in (0,1)$ also. Then, as noted in my comment on the question cited by the OP, we can write $$E\left[\frac{X}{X+Y}\right] + E\left[\frac{Y}{X+Y}\right] = E\left[\frac{X+Y}{X+Y}\right] = 1$$ and the above calculation is perfectly valid here whereas it was incorrect in what I had written in my comment on the previous question. If $X$ and $Y$ are independent and identically distributed, then symmetry allows to claim that $E\left[\frac{X}{X+Y}\right] = E\left[\frac{Y}{X+Y}\right]$ and we get that $$E\left[\frac{X}{X+Y}\right] = E\left[\frac{Y}{X+Y}\right] = \frac 12.$$ If $X$ and $Y$ are independent but not identically distributed, then we have to work harder. We need to calculate $$\int_0^\infty\int_0^\infty \frac{x}{x+y} f_X(x)f_Y(y) \,\mathrm dx \, \mathrm dy$$ (assuming $X$ and $Y$ are continuous random variables with densities $f_X(x)$ and $f_Y(y)$ respectively). This is an exercise in integration.

Answer 2

Summary

Suppose the problem is described as follows: $X$ and $Y$ have a bivariate normal distribution with respective parameters $\mu_X$, $\mu_Y$, $\sigma_X$, $\sigma_Y$, and $\rho$ and it is desired to find the mean of $R=X/(X+Y)$ given that $X>0$ and $Y>0$, then using Mathematica I was only able to find a symbolic result for $E(R|X>0, Y>0)$ when $\mu_X=\mu_Y=0$. Short of that there is a symbolic result for the density of $R$ given $X>0$ and $Y>0$ which then numerical integration can be used. Both of these results match means found from random sampling.

Case 1: $\mu_X=\mu_Y=0$

distxy = BinormalDistribution[{0, 0}, {\[Sigma]x, \[Sigma]y}, \[Rho]];
distPositive = TruncatedDistribution[{{0, \[Infinity]}, {0, \[Infinity]}}, distxy];
dR = TransformedDistribution[x/(x + y), {x, y} \[Distributed] distPositive, 
   Assumptions -> {\[Sigma]x > 0, \[Sigma]y > 0, \[Mu]x \[Element] Reals, \[Mu]y \[Element] Reals}];
pdf00 = PDF[dR, z]

The result for the pdf is

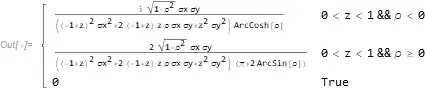
I don't know why but the first line of the result is wrong because it doesn't integrate to 1. (And while it looks like it involves imaginary numbers, the resulting density is real and positive. I've written Mathematica about it not integrating to 1. It turns out aht the second line of the equation does work for all values of $\rho$.)

So the pdf for $-1\lt \rho < 1$ is

$$\frac{2 \sqrt{1-\rho ^2} \sigma_X \sigma_Y}{\left(2 \sin ^{-1}(\rho )+\pi \right) \left(\sigma_Y^2 z^2+2 \rho \sigma_X \sigma_Y (z-1) z+\sigma_X^2 (z-1)^2\right)}$$

The mean is found with

Integrate[z (2 Sqrt[1 - \[Rho]^2] \[Sigma]x \[Sigma]y)/(((-1 + z)^2 \[Sigma]x^2 + 
  2 (-1 + z) z \[Rho] \[Sigma]x \[Sigma]y + z^2 \[Sigma]y^2) (\[Pi] + 2 ArcSin[\Rho]])),
  {z, 0, 1}, Assumptions -> {\[Sigma]x > 0, \[Sigma]y > 0, -1 < \[Rho] < 1}]

and results in

$$\frac{2 \sigma_X \left(\sqrt{1-\rho ^2} \sigma_Y \log \left(\frac{\text{$\sigma $y}}{\sigma_X}\right)+(\rho \sigma_Y+\sigma_X) \tan ^{-1}\left(\frac{\rho \sigma_X+\sigma_Y}{\sqrt{1-\rho ^2} \sigma_X}\right)+(\rho \sigma_Y+\sigma_X) \tan ^{-1}\left(\frac{\rho \sigma_Y+\sigma_X}{\sqrt{1-\rho ^2} \sigma_Y}\right)\right)}{\left(2 \sin ^{-1}(\rho )+\pi \right) \left(2 \rho \sigma_X \sigma_Y+\sigma_X^2+\sigma_Y^2\right)}$$

As a partial check on this consider finding the mean from random sampling:

(* Set parameters *)
parms = {\[Sigma]x -> 1, \[Sigma]y -> 3, \[Rho] -> -6/7};

(* Theoretical mean *)
(2 \[Sigma]x ((\[Sigma]x + \[Rho] \[Sigma]y) ArcTan[(\[Rho] \[Sigma]x + \[Sigma]y)/
  (Sqrt[1 - \[Rho]^2] \[Sigma]x)] + (\[Sigma]x + \[Rho] \[Sigma]y) ArcTan[(\[Sigma]x + 
  \[Rho] \[Sigma]y)/(Sqrt[1 - \[Rho]^2] \[Sigma]y)] + 
  Sqrt[1 - \[Rho]^2] \[Sigma]y Log[\[Sigma]y/\[Sigma]x]))/
  ((\[Sigma]x^2 + 2 \[Rho] \[Sigma]x \[Sigma]y + \[Sigma]y^2) (\[Pi] + 2 ArcSin[\Rho]])) 
  /. parms // N
(* 0.322394 *)

(* Mean from random sampling *)
n = 1000000;
distxy = BinormalDistribution[{0, 0}, {\[Sigma]x, \[Sigma]y}, \[Rho]];
distPositive = 
  TruncatedDistribution[{{0, \[Infinity]}, {0, \[Infinity]}}, distxy];
xy = RandomVariate[distPositive /. parms, n];
ratio = #[[1]]/Total[#] & /@ xy;
Mean[ratio]
(* 0.322567 *)

So they match pretty well.

Case 2: $\rho=0$

Here I could find only the symbolic result for the density of $R|X>0, Y>0$.

distxy = BinormalDistribution[{\[Mu]x, \[Mu]y}, {\[Sigma]x, \[Sigma]y}, 0];
distPositive = TruncatedDistribution[{{0, \[Infinity]}, {0, \[Infinity]}}, distxy];
dR = TransformedDistribution[x/(x + y), {x, y} \[Distributed] distPositive, 
   Assumptions -> {\[Sigma]x > 0, \[Sigma]y > 0, \[Mu]x \[Element] Reals, \[Mu]y \[Element] Reals}];
pdf0 = PDF[dR, z]

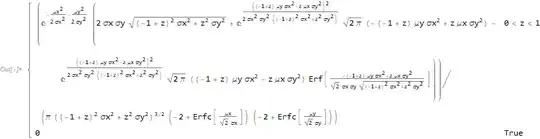
Given that the error functions (Erf[] and Erfc[] = 1- Erf[] which are functions of the cumulative normal distribution function) are part of the density, it is unlikely that a general symbolic result for the mean exists. But we can use numerical integration to find the mean for an set of parameters.

parms = {\[Mu]x -> 1, \[Mu]y -> 3, \[Sigma]x -> 2, \[Sigma]y -> 7};
NIntegrate[z pdf0 /. parms, {z, 0, 1}]
(* 0.286721 *)

(* Mean from random sampling *)
n = 1000000;
distxy = BinormalDistribution[{\[Mu]x, \[Mu]y}, {\[Sigma]x, \[Sigma]y}, 0] /. parms;
distPositive = TruncatedDistribution[{{0, \[Infinity]}, {0, \[Infinity]}}, distxy];
SeedRandom[12345];
xy = RandomVariate[distPositive /. parms, n];
ratio = #[[1]]/Total[#] & /@ xy;
Mean[ratio]
(* 0.286566 *)

These results also match.

General case

It would seem that for other combinations of parameters not contained in the first 2 cases, one would need random sampling to approximate the conditional mean. (I'd like to be wrong about that.)