Having lost some of my math skills, I am having problems with something that I think should be fairly easy but is eluding me:
I have a plateau shaped function that I would like to standardise such that regardless of the a, b and alpha values and x it always produces a value between 0.2 and 1. It is easy in R to rescale a series of values but not single values.
Function in R
plat.f = function(x, a, b, alpha){
y = log((cosh(2*alpha*pi*a)+cosh(2*alpha*pi* x))/(cosh(2*alpha*pi*b)+cosh(2*alpha*pi*x)))
y = y/pi/alpha/6
return(y)
}
curve(plat.f(x, 6, 3, 0.6),-10,10)
[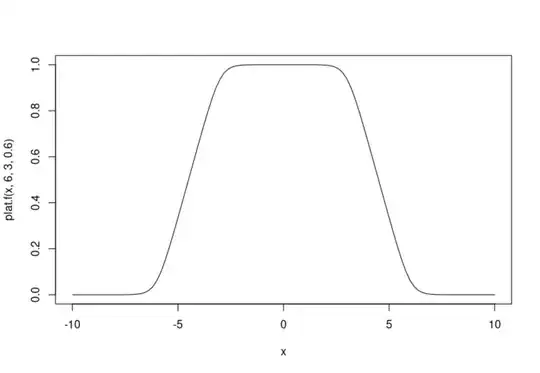 ]
]
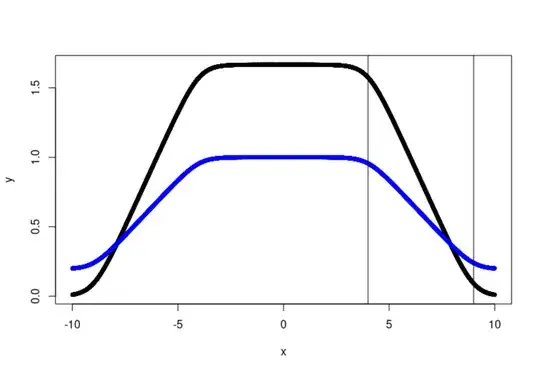
So what I want is that regardless of what values of a, b and alpha I give it will have a value between 0.2 and 1 while right now it is between 0 and a value determined by a and b parameters. So when x=0 I want y=1 and when x=-10 I want y=0.2 and when x=5, y should be somewhere around between 0.33 and 1 while right now it is 0.33.
Edit: Here is some more context and code. If I generate a series from the plateau function with random x between -10 and 10, I will get a series of y values that I can rescale. This rescaled series maintains the meaning of the a and b parameters with the rescaling (vertical lines) while the raw function (black) has a plateau at 1.66 and the rescaled (blue) has the max-min properties I want. I just need to figure out how to do this in the function as I will pull a sample from it with single random x values that I generate and those should follow a function with max, min values and the a and b meaning (in terms of where the plateau falls off and where the ends).
plat.f = function(x, a, b, alpha){
y = log((cosh(2*alpha*pi*a)+cosh(2*alpha*pi*x))/(cosh(2*alpha*pi*b)+cosh(2*alpha*pi*x)))
y = y/pi/alpha/6
return(y)
}
x=runif(10000,-10,10)
a=9
b=4
alpha=0.4
y=plat.f(x=x, a=a,b=b,alpha=alpha)
plot(x,y,pch=20)
y.rescaled= scales::rescale(y,c(0.2,1))
points(x,y.rescaled,pch=20,col="blue")
abline(v=a)
abline(v=b)