4

I want to find a way to fit a series of curves throught 2d data. I have a hypothsis of how this can be done (I will explain it below). I would appreciate if anyone could suggest whether this technique has a name and whether there is a tool that does it allready (R/Python/Matlab/Mathematica are all welcome). Ideally I would like to generalize it to many dimensions.

Single curve through 2d data

In an ideal world my 2d data would nicely fit into some 1d curve, e.g.:

Figure 1. 2D data fits single 1d curve

To find fit for such data one could use regularized polynomial regression, for example.

NB! The special thing about this data is that it is a result of optimization that aims to get low $f_1$ and low $f_2$, thus, in general, data tends to follow curves that start somewhere high on axis $f_2$ and then decay towards axis $f1$ without crossing the origin.

Many curves through 2d data

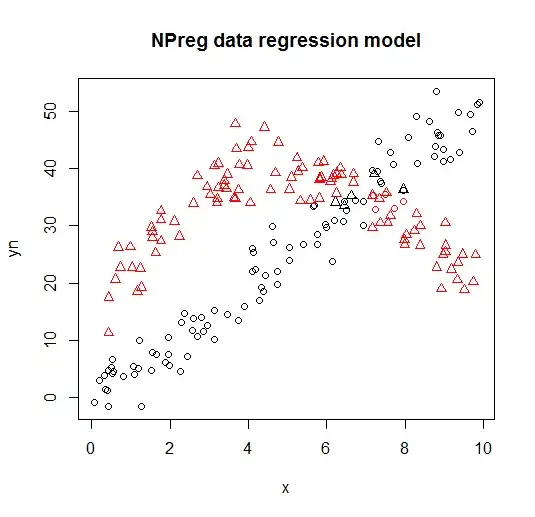
Instead my data looks more like in sub-figure (a) below:

Figure 2: The data consists out of three merged datasets. Each dataset can be fitted by a different curve.

My hypothesis is that there exists a way to partition this data in a way shown in sub-figure (b) above.

My approach

I understand that it may be impossible to regenerate the curves in Figure 2b. That's not the aim. The aim is to find relationships between $f_1$ and $f_2$ by postulating that such relationships exist and then trying to learn ways to partition the data in such a way as to extract these relationships.

My algorithm would be to:

  1. Fit a curve with e.g. 5 vertices, one of them lying on axis $f_1$, another on axis $f_2$, in such a way that half of the data is below the curve and half is above.

  2. Repeat the algorithm (recursively) for upper and lower halves of the data.

Rough illustration is as follows:

enter image description here

The stopping criterion would be either the thickness of the partitioned region, or the number of data points in it.

Conclusion

Coming back to the questions at the start of the post. Does this approach make sense? Does it ring a bell?

THANKS!

Cryo
  • 336
  • 1
  • 6
  • "Bisect" means to split into *two,* which is somewhat misleading. What you are describing in your approach sounds very much like *quantile regression* -- but that won't solve the problem you state. In general cases this problem looks like it has no clear solution, suggesting that anything you can do to narrow or constrain the situation could help. – whuber May 12 '20 at 16:05
  • @whuber Thanks! Indeed, the splitting in two did remind me of median a lot. – Cryo May 12 '20 at 16:14

1 Answers1

2

You could try the mixture of regression models (cluster-wise regression), i.e. an algorithm that clusters your data into some finite number of subsets, where each cluster is defined by it's own regression model. Below you can find example from the linked thread, that shows two such clusters found the algorithm in some synthetic data.

enter image description here

Tim
  • 108,699
  • 20
  • 212
  • 390