4

I have tried to create a predictive model based on the probit model (common in my field). The model is given as:

$$\operatorname{Prob} = \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{t}\exp\left(-\frac{x^2}{2}\right)\,dx,$$

and includes three parameters:

$$ t = \frac{M-k}{l k} $$

In this case the value of $l$ tells you something about the slope of the curve, the $k$ is where the 50% probability is, and $M$ are the values on the $x$-axis calculated from the third parameter $j$.

The model parameters was found through maximum likelihood estimation, where I have a grid/range of the different parameters, which I cycled through, and then through MLE I found the best-fit parameters.

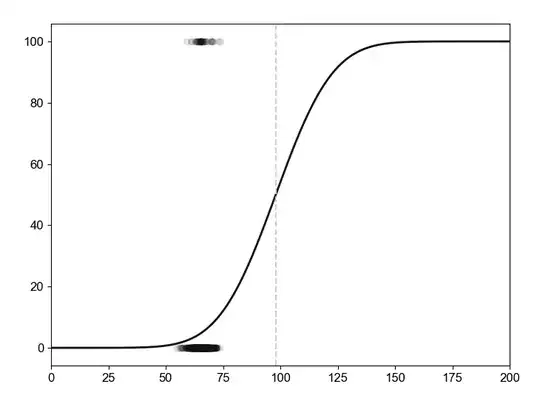
However, when plotting the curve from the best-fit parameters, calculate the the $M$ value for each case, and put them at 0% or 100% depending on the case being an event or not ($0$ or $1$), it just doesn't seem to add up to me (see figure below).

The dashed line indicates the $k$ value found from the MLE. The slope ($l$) is probably alright, but again, by looking at the events which are between $50-75$ in this case, shouldn't the $50\%$ line be more located around there instead of around $100?$

It should be mentioned, that my confidence intervals from bootstrapping are very broadin this case. So there are obviously some kind of problem here. I just can't seem to figure out what?

enter image description here

Denver Dang
  • 787
  • 4
  • 15
  • 1
    This might be related to your apparent class imbalance in the data - with imbalanced data, you may need to move your decision threshold to something other than 0.5. See https://stats.stackexchange.com/questions/6067/does-an-unbalanced-sample-matter-when-doing-logistic-regression – Nuclear Hoagie May 12 '20 at 15:01
  • The problem is that in this case (this model), the 50% threshold is what has been used for decades. Shifting it would make it less comparable to other models derived from the same model and parameters. But if I understand correctly, the reason this happens/can happen, is because my data is imbalanced. So as such, there isn't much to do about it, other than shifting the decision threshold, or by doing another type of models, where I include other/better predictors ? – Denver Dang May 12 '20 at 16:46

0 Answers0