0

I have a data series that increases exponentially at the beginning and then reaches a plateau, like in a chemical reaction. I would like to find the point where the exponential phase finishes. 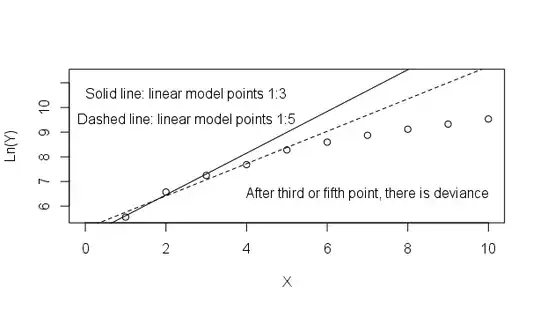I transformed the data into their natural logarithms in order to obtain a linear series for the exponentially rising data and I am looking for the first outlier of the linear series first outlier that wil pinpoint the end of the exponential phase, as shown in this figure: enter image description here

I can calculate the residuals of the linear models (here Y is already transformed in ln(Y):

mod_3 = lm(Y[1:3] ~ X[1:3])
res_3 = mod_3$residuals
mod_5 = lm(Y[1:5] ~ X[1:5])
res_5 = mod_5$residuals
mod_6 = lm(Y[1:6] ~ X[1:6])
res_6 = mod_6$residuals
> print(res_3)
          1           2           3 
-0.05724195  0.11448390 -0.05724195 
> print(res_5)
          1           2           3           4           5 
-0.20016682  0.16104238  0.17879988 -0.04005963 -0.09961581 
> print(res_6)
          1           2           3           4           5           6 
-0.28407154  0.14006620  0.22075225  0.06482127  0.06819364 -0.20976181 
>

My question is: how can I test that a given point (let's say point 6 by the look of the data) is significantly deviant from a linear model?

For instance, if I keep the linear model between points 1 and 3, how can I tell if points 4 or 6 are significantly divergent from the estimate? That is: how can I tell if a point is an outlier?

I need to find the minimal number of points that makes a linear series; if I add more and more points, there should be a point where R^2 becomes too big, but the residuals might still be small. For instance, the residual for point 6 is -0.21 in the linear model build on the points 1:6; but 

> Y[6]
[1] 8.59471
> mean(Y[1:3])
[1] 6.459196
> Y[6]-mean(Y[1:3])
[1] 2.135513

The problem is how to demonstrate that I should keep the points 1 to 3 as generators of a linear series.

ADDENDUM

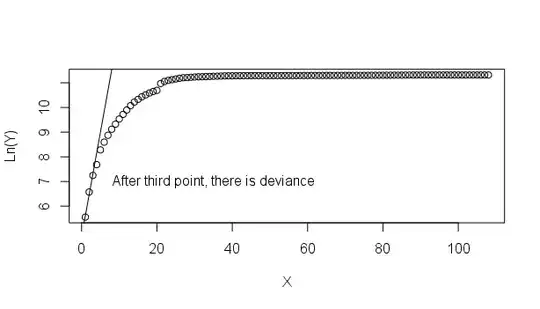
To give a better context, I am adding the whole plotting of the data: enter image description here

Also, the idea of identifying the first outlier in a linear series is drawn directly from an article written by Tichopad et al. (Nucleic Acids Research, Volume 31, Issue 20, 15 October 2003, Page e122). In this paper, the values are those of the fluorescence in a polymerase chain reaction, which pass from linear to exponential to plateau as in this figure: enter image description here

But instead of looking at the change in the cycles 1-16, I am looking for that in the cycles 20-30. To find the first outlier, a series of statistical parameters were calculated, which included an ‘externally studentized’ residual, the mean square residual of the regression model with the deleted inspected data point, the distribution of the studentized residuals, and the cumulative function of the studentized residuals. The probability that spots an outlier is given by P‐value = 2 × [1 – F(1 – |r(n – 1)|)], with F the cumulative function, r the ‘externally studentized’ residual and n the point in evaluation.

Gigiux
  • 139
  • 6
  • 1
    The premise here seems contradictory to me, in so far as you are postulating smooth change but also playing with the idea of a changepoint at which behaviour shifts from one phase to another. It's usually better to try to model the entire series to see how well that works. Much of the point about e.g. logistic curves is that values and all derivatives change smoothly throughout the range. – Nick Cox May 12 '20 at 07:32
  • I think there can be smooth change but at some point the exponential progression (or linear in the logarithmic transformation) will become something else otherwise there would be no plateau phase. The problem is how to find that crucial point... – Gigiux May 12 '20 at 11:23
  • 1
    I fear you are missing the point. You can't have it both ways Either you think your curve is segmented, in which case fix a model with spline-like segments that join, or else talk or thinking of phases is just psychological, and nothing to do with the mathematics or statistics. If your examples are typical, you don't have enough data to distinguish well between different kinds of variation any way. – Nick Cox May 12 '20 at 12:27
  • OK, so I should try to fit a spline to the data and see if it comes segmented? – Gigiux May 12 '20 at 13:02
  • Maybe the deviant is the first point ? – Rodolphe May 12 '20 at 13:10
  • Whether a composite fit shows visibly distinct segments depends on what you fit. For example, a cubic spline is _defined_ to have values and the first two derivatives changing continuously. Again, I am not clear whether you have enough data points for that to work well. In other threads, a monotone spline has been recommended. – Nick Cox May 12 '20 at 13:16
  • https://stats.stackexchange.com/questions/341567/how-to-get-value-of-y-for-a-given-value-of-x-for-a-curve seems closer to your question than the title may appear to imply. – Nick Cox May 12 '20 at 13:17

0 Answers0