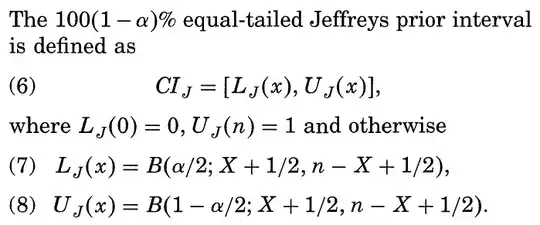I have two data sets, A and B, and I have linked them together using automatic, probabilistic methods to create a set of linked records (L). For example, my code could have predicted that record 1 in set A most likely refers to the same item as record 3 in set B. I then took a small sample from set A and found the correct record from B for each of these items. I’ll call this set of checked linked records the gold standard (G). I can then use G to check L.
Using true positives (TP), the number of times that G is the same as L, and false positives (FP), the number of times that G is not the same as L, the positive predictive value (PPV), TP/(TP+FP), measures the proportion of classified matches that are correctly identified as such. In the record linkage and classification literature It is referred to as precision but it is not analogous to the closeness of a set of measurements to each other and so to avoid confusion I will refer to it as PPV. Where a representative sample of a population is tested, PPV is a prediction of the positive post-test probability; the probability of the presence of a condition after a positive diagnostic test, or in record linkage, the probability that each pair of linked records (POLR) is correct.
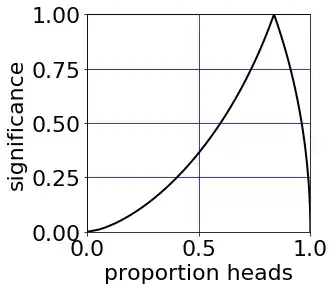
I can predict confidence intervals and the distribution of PPV with a bootstrap; that is by sampling from G with replacement. But consider the case where I get a PPV of 1. That would indicate that each POLR in G is predicted correctly in L. But while I am happy to assume that G is perfectly correct, I don’t want to assume that it is perfectly representative of L, which is a vastly larger set. How can I adjust my bootstrap to take account of the possibility (it is highly likely) that my sample is not perfectly representative of the total population please?