The standard justification for manifold learning is that the map from the latent to observed spaces is nonlinear. For example, here is how another StackExchange user justified Isomap over PCA:
Here we are looking for 1-dimensional structure in 2D. The points lie along an S-shaped curve. PCA tries to describe the data with a linear 1-dimensional manifold, which is simply a line; of course a line fits these data quite bad. Isomap is looking for a nonlinear (i.e. curved!) 1-dimensional manifold, and should be able to discover the underlying S-shaped curve.
However, in my experience, either PCA does comparably well to a nonlinear model or the nonlinear model also fails. For example, consider this result:
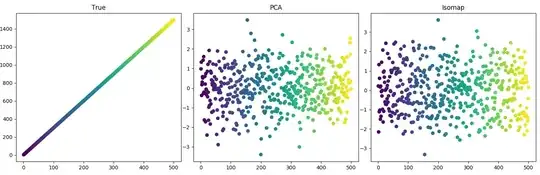
A simple latent variable changes over time. There are three maps into observation space. Two are noise; one is a sine wave (see Code 1 below). Clearly, a large value in observation space does not correspond to a large $x$ value in latent space. Here is the data colored by index:
In this case, PCA does as well as Isomap. My first question: Why does PCA do well here? Isn't the map nonlinear?
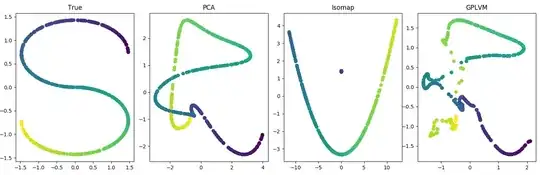
You might say this problem is too simple. Here's a more complicated example. Let's introduce two nonlinearities: a nonlinear latent space and a nonlinear maps. Here, the latent variable is shaped like an "S". And the maps are GP distributed, meaning if there are $J$ maps, each $f_j(x) \sim \mathcal{N}(0, K_x)$, where $K_x$ is the covariance matrix based on the kernel function (see Code 2 below). Again, PCA does well. In fact, the GPLVM whose data generating process is being matched exactly appears to not deviate much from its PCA initialization:
So again I ask: What's going on here? Why am I not breaking PCA?
Finally, the only way I can break PCA and still get something a bit structured from a manifold learner is if I literally "embed" the latent variable into a higher dimensional space (see Code 3 below):
To summarize, I have a few questions that I assume are related to a shared misunderstanding:
Why does PCA do well on a simple nonlinear map (a sine function)? Isn't the modeling assumption that such maps are linear?
Why does PCA do as well as GPLVM on a doubly nonlinear problem? What's especially surprising is that I used the data generating process for a GPLVM.
Why does the third case finally break PCA? What's different about this problem?
I appreciate this is a broad question, but I hope that someone with more understanding of the issues can help synthesize and refine it.
EDIT:
PCA on a latent variable that is not linearly separable and with nonlinear maps:
Code
1. Linear latent variable, nonlinear map
import matplotlib.pyplot as plt
import numpy as np
from sklearn.decomposition import PCA
from sklearn.manifold import Isomap
def gen_data():
n_features = 3
n_samples = 500
time = np.arange(1, n_samples+1)
# Latent variable is a straight line.
lat_var = 3 * time[:, np.newaxis]
data = np.empty((n_samples, n_features))
# But mapping functions are nonlinear or nose.
data[:, 0] = np.sin(lat_var).squeeze()
data[:, 1] = np.random.normal(0, 1, size=n_samples)
data[:, 2] = np.random.normal(0, 1, size=n_samples)
return data, lat_var, time
data, lat_var, time = gen_data()
lat_var_pca = PCA(n_components=1).fit_transform(data)
lat_var_iso = Isomap(n_components=1).fit_transform(data)
fig, (ax1, ax2, ax3) = plt.subplots(1, 3)
fig.set_size_inches(20, 5)
ax1.set_title('True')
ax1.scatter(time, lat_var, c=time)
ax2.set_title('PCA')
ax2.scatter(time, lat_var_pca, c=time)
ax3.set_title('Isomap')
ax3.scatter(time, lat_var_iso, c=time)
plt.tight_layout()
plt.show()
2. Nonlinear latent variable, GP-distributed maps
from GPy.models import GPLVM
import matplotlib.pyplot as plt
import numpy as np
from sklearn.decomposition import PCA
from sklearn.datasets import make_s_curve
from sklearn.manifold import Isomap
from sklearn.metrics.pairwise import rbf_kernel
def gen_data():
n_features = 10
n_samples = 500
# Latent variable is 2D S-curve.
lat_var, time = make_s_curve(n_samples)
lat_var = np.delete(lat_var, obj=1, axis=1)
lat_var /= lat_var.std(axis=0)
# And maps are GP-distributed.
mean = np.zeros(n_samples)
cov = rbf_kernel(lat_var)
data = np.random.multivariate_normal(mean, cov, size=n_features).T
return data, lat_var, time
data, lat_var, time = gen_data()
lat_var_pca = PCA(n_components=2).fit_transform(data)
lat_var_iso = Isomap(n_components=2).fit_transform(data)
gp = GPLVM(data, input_dim=2)
gp.optimize()
lat_var_gp = gp.X
fig, (ax1, ax2, ax3, ax4) = plt.subplots(1, 4)
fig.set_size_inches(20, 5)
ax1.set_title('True')
ax1.scatter(lat_var[:, 0], lat_var[:, 1], c=time)
ax2.set_title('PCA')
ax2.scatter(lat_var_pca[:, 0], lat_var_pca[:, 1], c=time)
ax3.set_title('Isomap')
ax3.scatter(lat_var_iso[:, 0], lat_var_iso[:, 1], c=time)
ax4.set_title('GPLVM')
ax4.scatter(lat_var_gp[:, 0], lat_var_gp[:, 1], c=time)
plt.tight_layout()
plt.show()
3. Nonlinear latent variable embedded into higher dimensional space
from GPy.models import GPLVM
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import make_s_curve
from sklearn.decomposition import PCA
from sklearn.manifold import Isomap
def gen_data():
n_features = 10
n_samples = 500
# Latent variable is 2D S-curve.
lat_var, time = make_s_curve(n_samples)
lat_var = np.delete(lat_var, obj=1, axis=1)
lat_var /= lat_var.std(axis=0)
# And maps are GP-distributed.
data = np.random.normal(0, 1, size=(n_samples, n_features))
data[:, 0] = lat_var[:, 0]
data[:, 1] = lat_var[:, 1]
return data, lat_var, time
data, lat_var, time = gen_data()
lat_var_pca = PCA(n_components=2).fit_transform(data)
lat_var_iso = Isomap(n_components=2).fit_transform(data)
gp = GPLVM(data, input_dim=2)
gp.optimize()
lat_var_gp = gp.X
fig, (ax1, ax2, ax3, ax4) = plt.subplots(1, 4)
fig.set_size_inches(20, 5)
ax1.set_title('True')
ax1.scatter(lat_var[:, 0], lat_var[:, 1], c=time)
ax2.set_title('PCA')
ax2.scatter(lat_var_pca[:, 0], lat_var_pca[:, 1], c=time)
ax3.set_title('Isomap')
ax3.scatter(lat_var_iso[:, 0], lat_var_iso[:, 1], c=time)
ax4.set_title('GPLVM')
ax4.scatter(lat_var_gp[:, 0], lat_var_gp[:, 1], c=time)
plt.tight_layout()
plt.show()
4. Latent variable that is not linearly separable with GP-distributed maps
from GPy.models import GPLVM
import matplotlib.pyplot as plt
import numpy as np
from sklearn.decomposition import PCA
from sklearn.datasets import make_circles
from sklearn.manifold import Isomap
from sklearn.metrics.pairwise import rbf_kernel
def gen_data():
n_features = 20
n_samples = 500
lat_var, time = make_circles(n_samples)
mean = np.zeros(n_samples)
cov = rbf_kernel(lat_var)
data = np.random.multivariate_normal(mean, cov, size=n_features).T
return data, lat_var, time
data, lat_var, time = gen_data()
lat_var_pca = PCA(n_components=2).fit_transform(data)
lat_var_iso = Isomap(n_components=2).fit_transform(data)
gp = GPLVM(data, input_dim=2)
gp.optimize()
lat_var_gp = gp.X
fig, (ax1, ax2, ax3, ax4) = plt.subplots(1, 4)
fig.set_size_inches(20, 5)
ax1.set_title('True')
ax1.scatter(lat_var[:, 0], lat_var[:, 1], c=time)
ax2.set_title('PCA')
ax2.scatter(lat_var_pca[:, 0], lat_var_pca[:, 1], c=time)
ax3.set_title('Isomap')
ax3.scatter(lat_var_iso[:, 0], lat_var_iso[:, 1], c=time)
ax4.set_title('GPLVM')
ax4.scatter(lat_var_gp[:, 0], lat_var_gp[:, 1], c=time)
plt.tight_layout()
plt.show()