0

How is the MLE for n calculated if p and k are given? I've been stuck on this forever and cannot seem to even find a similar example of calculating MLE of n.

taco
  • 3
  • 1
  • 1
    See also https://stats.stackexchange.com/questions/123367/estimating-parameters-for-a-binomial/123748#123748 – kjetil b halvorsen May 09 '20 at 05:31
  • 1
    You can avoid votes to 'close' a textbook question by showing what you have tried and why you need help. Also, a 'self-study' tag seems appropriate. Perhaps 'take the tour' of our site. – BruceET May 09 '20 at 05:45

1 Answers1

0

First, $k = 25$ and $p = 1/19,$ so the method-of-moments estimator (MME) is $k/p = 475.$ We don't know whether the maximum likelihood estimator is the same, but it may be similar. I will do a grid search in R, where a binomial PDF is denoted dbinom, to find the MLE. 

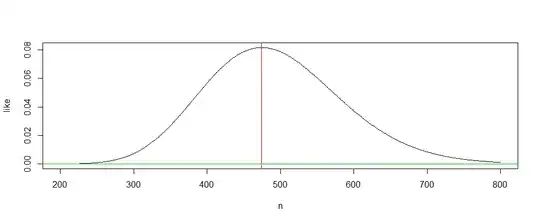
p = 1/19;  k = 25;  n = 200:800
like = dbinom(k, n, p)
mle = n[like==max(like)];  mle
[1] 474
plot(n, like, type = "l")
 abline(v = mle, col="red")
 abline(h=0, col="green2")

enter image description here

Check for uniqueness (because R rounds to some number of places):

like[n==474]
[1] 0.08170127
like[n==475]
[1] 0.08170127

So the MLE is either 474 or 475. We might as well use the MME. I will leave it to you to provide an analytic argument that this answer is correct. (For discrete quantities, a common approach to find a maximum is to look at ratios.)

Of course, all of this assumes that the usual rules of probability apply to extraordinarily beautiful Eastern European princesses playing roulette at the Bellagio.

BruceET
  • 47,896
  • 2
  • 28
  • 76