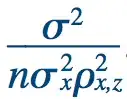Wald wrote his analysis in a set of eight technical memoranda for the Statistical Research Group (SRG), and these documents have been published by the Centre for Naval Analysis, so you can actually read them and see exactly what he did in his written work. The original memos can be found here and a good summary and analysis of his work on survival of aircraft is set out in Mangel and Samaniego (1984). If you read this paper and the accompanying technical memos you will see that Wald did indeed develope a theoretical model of aircraft survival to make his conclusions.
Wald's analysis covered multiple problems, starting with estimation of the survival probabilities for aircraft based on the number of hits to those aircraft, and then proceeding in more detail to estimation based on the number and location of the hits. His method goes essentially like this. For any plane that leaves on a bombing run, there is a distribution for the number of hits that plane will take. For any given number of hits there is an associated survival probability; a plane with no hits is assumed to survive with probability one, and the conditionla probability of survivial from each hit is some positive probability. Based on this, it is possible to use data on the returning planes to estimate the conditional probabilities of survival for each hit. (Any plane that does not return is assumed to have been hit at least once, and is missing data.)
To deal with different probabilities for hits to different locations, Wald expanded his model to divide the plane into a finite number of locations, and expanded the model so that there is an unknown conditional probability of survival for each hit to each location. Wald assumed that the conditional distribution of hits to specific locations (given the total number of hits) was known. He advanced the view that this could be determined experimentally within the military research centres by firing dummy bullets at real aircraft. Given assumed values for these probabilties (based on independent experiments), and some sensible statistical independence assumptions, you can then use the data on the number and locations of hits on returning planes to estimate the conditional probabilities of survival for each hit on a particular location. (Again, any plane that does not return is assumed to have been hit at least once, and is missing data.) If you formulate a model like this, the phenomenon under consideration here will emerge --- i.e., the more hits observed on a particular location, the higher the estimated survival probability for hits on that location will be. Thus, the parts of the aircraft showing the lowest survivial probability for hits will be those that have the lowest number of hits in the returning planes (relative to the probability of being hit in that location).
Wald's technical memoranda on this subject give specific formulae for his models and estimation methods for the unknown conditional probabilities. Nevertheless, it is not necessary to understand the technical details to understand his basic insight that areas of the plane exhibiting low numbers of hits (on the returning planes) are actually the most vulnerable parts. The reason this story is so wonderful is that it illustrates a counter-intuitive problem involving missing data where the intuitive answer for most people is the opposite of the correct answer. I have used this problem as a teaching example in statistics seminars a number of times, and when asked their advice, the audience inevitably advise that more armour should be attached to the parts of the planes that showed the most damage in the data. When they are informed of Wald's opposite advice, and the reasoning for it, they are usually very impressed.
Finally, with regard to the actual folk legend that has emerged around this, I am not aware of any evidence showing exactly what conversations Wald had with the military, what he said, or who disagreed with him (or was surprised by his advice). However, in the versions of the story I have heard, it was not other statisticians he was disagreeing with, but military officials who lacked the statistical training needed to have the intuitively correct answer to this missing data problem. In any case, it is a brilliant story about a brilliant man.