Suppose $n = 5$, $s = 0.0771$.
The question is: what's the $P(\sigma < 7.63\%)$?
Suppose $n = 5$, $s = 0.0771$.
The question is: what's the $P(\sigma < 7.63\%)$?
Is this question motivated by a concrete problem?
You can’t compute that if you don’t know anything on the distribution of the population. If it is normal, it is known that $s^2$ is drawn from a ${\sigma^2\over n-1}\chi^2(n-1)$.
Hence, interpreting your question as “what is $\def\P{\mathbb P} \P(S^2 \ge 0.0771^2)$ if $\sigma^2 = 0.0763^2$”, as is commonly done in the context of confidence intervals,
$$\begin{aligned}
\P(S^2 \ge 0.0771^2)
&= \P\left( 4 {S^2 \over \sigma^2} > 4 {0.0771^2 \over 0.0763^2}\right)\\
& =\P( X > 4.084 )
\end{aligned}$$
with $X \sim \chi^2(4)$. This is pchisq(4.084, df=4, lower.tail=FALSE) which is 39.4%.
Note on the interpretation of the question In a previous version of this answer, I made (and signaled) the following abuse of notation: $\P(\sigma^2 < 0.0763^2) = \P\left( \sigma^2 < {0.0763^2 \over 0.0771^2} S^2 \right)$, and then continued as above.
This is totally nonsensical in the frequentist setting, as (as stated by whuber in the comments) $\sigma$ is not a random variable, but a number. Hence, strictly speaking, $\P(\sigma^2 < 0.0763^2)$ is either 0 or 1, and one don’t know which. I think it would have been unfair to ask for a reformulation of the question, as the above reformulation is quite usual and linked to the pivot method for confidence interval. I think the question this would make sens in Fisher fiducial inference however I am not sure wether fiducial inference make sense at all. A rigorous answer could be made in the bayesian framework, assuming that the parameter $\sigma^2$ is drawn from some prior distribution.
Fiducial inference: distribution on $\sigma^2$ I may not gain friends with what follows... This is one of the cases where Fisher advocated that one can obtain for the unknown variance $\sigma^2$ a fiducial probability distribution, with no need of prior distribution, as follows.
$$\begin{aligned}
F(x) = \P(\sigma^2 < x) &= \P\left(X > 4 { 0.0771^2\over x^2} \right)\\
&= 1 - \P\left( X < {0.023778 \over x} \right)
\end{aligned}$$
where $X \sim \chi^2(4)$. Of course this is for $x>0$, if $x \le 0$ one let $F(x) = 0$. Then $F$ is continuous and increases from 0 to 1 on the real line; it is the cdf of the fiducial probability distribution of $\sigma^2$. Here is a graph of $F$ and its derivative $f$ (note the two different scales).
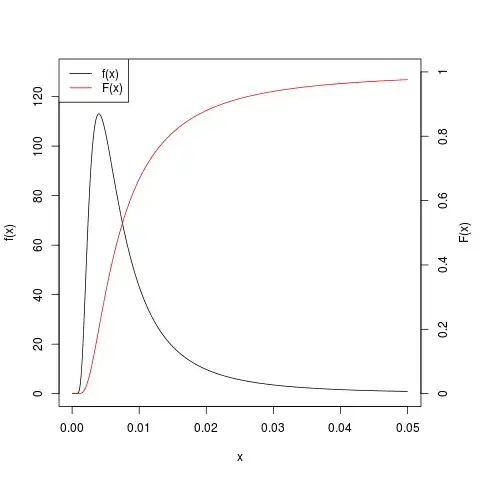
I know fiducial inference has flaws and is not much in favor anymore. However for simple questions like this one, which are very frequent from non-statisticians, it allows to give satisfactory answers, and matches well the intuition of non-math-statisticians about confidence intervals and regions.