What kind of distribution does this have?

Question

Currently I'm trying to figure out the distribution of the following:

$X \sim \frac{\sqrt{n}}{\sqrt{Gamma(n,\beta)}}$ where the denominator follows a $Gamma(n,\beta)$ distribution.

I've checked out these links:

1. Square root of an inverse gamma distributed random variable;
2. Square root of inverse gamma distribution?;
3. https://en.wikipedia.org/wiki/Inverse-gamma_distribution;
4. https://en.wikipedia.org/wiki/Nakagami_distribution.

I'm just not sure how to connect the dots. I think I'm playing with some kind of Nakagami distribution? Just trying to figure out a clean way of expressing $X$ and knowing what it's parameters would look like. I need to find it's mean and variance if I can.

Answer 1

The $\sqrt{n}$ term in the numerator only scales your random variable, so we can disregard it for now.

The square root of a gamma distributed variable is Nakagami distributed. We are looking for the reciprocal of that, which could be called an "inverse Nakagami distribution".

Louzada et al. (2018) looks like it might be helpful. It defines exactly the kind of inverse Nakagami you are looking for and gives a number of propositions, such as the moments. You would just need to scale them appropriately by your $\sqrt{n}$ scaling factor.

Answer 2

Let $Z$ have a Gamma$(n,1)$ distribution, which has density

$$f_Z(z) = \frac{1}{\Gamma(n)}\, z^{n-1} \,e^{-z}\,\mathrm{d}z.$$

Let $\lambda \gt 0.$ Then

$$X = \sqrt{\lambda}Z^{-1/2}$$

ranges from $0$ to $\infty$ and

$$Z = \frac{\lambda}{X^2}.$$

Substituting $z = \lambda x^{-2}$ and (therefore) $|\mathrm{d}z| = 2\lambda x^{-3}\mathrm{d}x$ we find

$$f_X(x)\mathrm{d}x = \frac{1}{\Gamma(n)} (\lambda x^{-2})^{n-1}\,e^{-\lambda/x^2}\,2\lambda x^{-3}\mathrm{d} x = \frac{2\lambda^{n}}{\Gamma(n)}\, x^{-2n-1}\,e^{-\lambda/x^2}\,\mathrm{d}x.$$

Set $\lambda = \sqrt{n/\beta}$ or $\lambda=\sqrt{n\beta}$ depending on whether $\beta$ is a scale or rate parameter, respectively.

This is a Generalized Inverse Gamma distribution.

---

To find the moments of $X$ it's simpler to ignore all this. Let $k$ be the moment ($k=1$ for the expectation, etc.) and observe

$$E(X^k) = E\left(\lambda^{k/2} Z^{-k/2}\right) = \lambda^{k/2} \frac{1}{\Gamma(n)}\int_0^\infty z^{-k/2}\,z^{n-1}\,e^{-z}\,\mathrm{d}z = \lambda^{k/2}\frac{\Gamma(n-k/2)}{\Gamma(n)}.$$

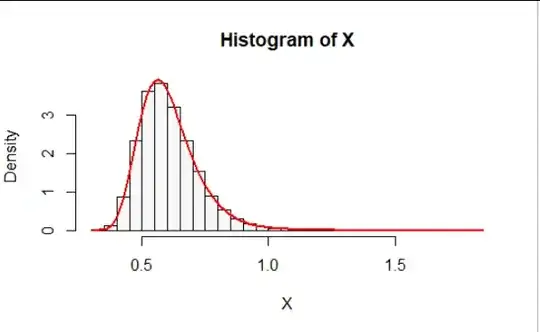
Here is a histogram for $10^5$ realizations of $Z$ with $n=8,$ $\beta=1/3$ (the rate). On it I have superimposed the theoretical distribution, which is in close agreement. The following R code reports the mean and variance of this sample and the theoretical values; they, too, agree closely.

n <- 8
beta <- 1/3
n.sim <- 1e5

Z <- rgamma(n.sim, n, beta)
X <- sqrt(n)/sqrt(Z)

hist(X, freq=FALSE, breaks=50, col="#f8f8f8")
curve(dgamma(n/x^2, n, beta) * 2*n/x^3, xname="x", add=TRUE, col="Red", lwd=2)

c(Mean=mean(X), Formula=sqrt(n*beta) * exp(lgamma(n-1/2) - lgamma(n)))
c(mu2=mean(X^2), Formula=n*beta / (n-1))
c(Variance=var(X), Formula=n*beta*(1/(n-1) - exp(2*(lgamma(n-1/2) - lgamma(n)))))