product of two probability density functions

Question

I have on one hand a z variable following a standard normal distribution N(0,1) and on the other hand a variable X following a Nakagami distribution. I am supposed to find a Gaussian distribution when I take the product of the two distributions described above. I can't find it as I am left with an expression resembling a gamma distribution inside the integral. Has anyone come across that kind of question? Are there different kinds of Nakagami distributions?

Answer 1

If $Y=b_0+Z/\sqrt{\lambda \tau}$ where $Z\sim N(0,1)$ and $\lambda$ has either a gamma distribution (with parameters $a$ and $b$) or a Nakagami distribution (with parameters $m$, and $w$), then Mathematica (and not my limited algebraic skills) finds the following pdf's for $\tau>0$ and assuming that $Z$ and $\lambda$ are independent:

d1 = TransformedDistribution[b0 + z/Sqrt[n \[Tau]], {z \[Distributed] NormalDistribution[0, 1], 
    n \[Distributed] GammaDistribution[a, b]}];
pdf1 = PDF[d1, z]

$$\frac{2^a \sqrt{b} \sqrt{\tau } \Gamma \left(a+\frac{1}{2}\right) \left(b \tau (b_0-z)^2+2\right)^{-a-\frac{1}{2}}}{\sqrt{\pi } \Gamma (a)}$$

d2 = TransformedDistribution[b0 + z/Sqrt[n \[Tau]], {z \[Distributed] NormalDistribution[0, 1], 
    n \[Distributed] NakagamiDistribution[m, w]}];
pdf2 = PDF[d2, z]

$$\frac{\sqrt{\tau } \sqrt[4]{\frac{w}{m}} \left(2 \Gamma \left(m+\frac{1}{4}\right) \, _1F_1\left(m+\frac{1}{4};\frac{1}{2};\frac{w (b_0-z)^4 \tau ^2}{16 m}\right)-\tau (b_0-z)^2 \sqrt{\frac{w}{m}} \Gamma \left(m+\frac{3}{4}\right) \, _1F_1\left(m+\frac{3}{4};\frac{3}{2};\frac{w (b_0-z)^4 \tau ^2}{16 m}\right)\right)}{2 \sqrt{2 \pi } \Gamma (m)}$$

Maybe you are directly integrating the product of the pdf's of $Z$ and $\lambda$ to obtain the pdf of $Y$ but it's all about how you do the integration which is why I think your title is misleading. I have chosen the lazy way (and most efficient for me).

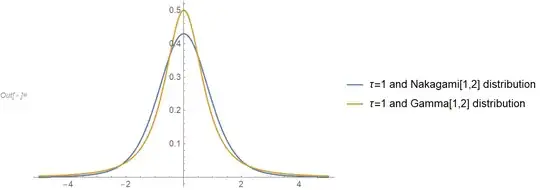
As an example consider $b_0=0$, $a=1$, $b=2$, $m=1$, $w=2$, and $\tau=1$:

Plot[{pdf1 /. {b0 -> 0, m -> 1, w -> 2, \[Tau] -> 1}, 
  pdf2 /. {b0 -> 0, a -> 1, b -> 2, \[Tau] -> 1}},
 {z, -5, 5}, WorkingPrecision -> 30,
 PlotLegends -> {"\[Tau]=1 and Nakagami[1,2] distribution",
   "\[Tau]=1 and Gamma[1,2] distribution"}]