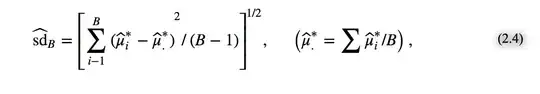Performing t-test for coefficients using bootstrap

Question

I am having some difficulties reconciling a test for the difference in means using a standard test and the bootstrap. It would be great if someone could tell me what is going wrong in the code.

I run two regressions on two different samples and obtain the following:

$b_1 = 0.02 \hspace{3mm} (0.09)$

$b_2 = -0.03 \hspace{3mm} (0.08)$

There are 8500 observations in each sample.

Based on the answer here, the t-statistic can be calculated using the standard error $s$ below:

\begin{equation} s =\sqrt{\frac{(n_1 - p)s_1^2 + (n_2 - p)s_2^2}{n_1 + n_2 - 2p}} \end{equation} With one regressor $p$, I did this by hand and I find that $s = 0.09$, so that the t-statistic would be $0.55$.

However, I also try to bootstrap the standard errors, I get a much smaller standard error ($0.03$). To give an idea of the process I am using:

1. Draw a bootstrap sample from group 1
2. Estimate the model using the data in step 1
3. Store the coefficient estimate as $b_1$
4. Draw a bootstrap sample from group 2
5. Estimate the model using the data in step 4
6. Store the coefficient estimate as $b_2$
7. Repeat the above 100 times

Then I perform a t-test on the two vectors containing $b_1$ and $b_2$. I suppose something is wrong in the steps above, but I don't know what it is. I am using bootstrap because I cannot include interaction terms in my model.

Thank you.

EDIT Here is the code I am using.

B<-50
t.vector1<-vector(length=B)
t.vector2<-vector(length=B)

for (j in 1:B){
boot.dat1<-data1[sample(nrow(data1),nrow(data1),replace=TRUE),]
boot.mod1<-rdrobust(y=boot.dat1$y,x=boot.dat1$x)

boot.dat2<-data2[sample(nrow(data2),nrow(data2),replace=TRUE),]
boot.mod2<-rdrobust(y=boot.dat2$y,x=boot.dat2$x,h=(boot.mod1$bws[1,1])) # local linear regression, so I use the same bandwidth as mod1

t.vector1[j]<-boot.mod1$Estimate[1,1]
t.vector2[j]<-boot.mod2$Estimate[1,1]
        }

ttest<-t.test(t.vector1,t.vector2)
ttest$stderr
[1] 0.02295152

Answer 1

The nonparametric bootstrap estimate of standard error for $\hat\mu$ (see review equation2.4 ):

which is basically the unbiased estimate of the standard deviation of $\mu$. In the t.test() function, stderr is a pooled estimate of the standard error of the mean, which is basically $\hat{sd}_{B} / \sqrt(B) $.

To get back your t-statistic, you need to plug in $\hat{sd}_{B}$ as the estimate of your standard error. Use some simulated data:

calculate_s = function(n1,s1,n2,s2,p=1){
sqrt(((n1 - p)*s1^2 + (n2 - p)*s2^2)/(n1+n2-2*p))
}

library(rdrobust)
set.seed(111)
x<-runif(1000,-1,1)
y1<-5+3*x+2*(x>=0)+rnorm(1000)
y2<-5+4*x+2*(x>=0)+rnorm(1000)

obs1 = rdrobust(y1,x)$Estimate
obs2 = rdrobust(y2,x)$Estimate

Not very sure how you obtain the standard error from the estimate, I am guessing it is "se.u". So we get an estimate of the pooled standard error like below:

calculate_s(1000,obs1[3],1000,obs2[3])
[1] 0.2241322

We run your bootstrap

B<-100
t.vector1<-vector(length=B)
t.vector2<-vector(length=B)

data1 = data.frame(x=x,y=y1)
data2 = data.frame(x=x,y=y2)

for (j in 1:B){
boot.dat1<-data1[sample(nrow(data1),nrow(data1),replace=TRUE),]
boot.mod1<-rdrobust(y=boot.dat1$y,x=boot.dat1$x)

boot.dat2<-data2[sample(nrow(data2),nrow(data2),replace=TRUE),]
boot.mod2<-rdrobust(y=boot.dat2$y,x=boot.dat2$x,h=(boot.mod1$bws[1,1])) 

t.vector1[j]<-boot.mod1$Estimate[1,1]
t.vector2[j]<-boot.mod2$Estimate[1,1]
        }

And calculate the standard error:

calculate_s(1000,sd(t.vector1),1000,sd(t.vector2))
[1] 0.3471487

This is closer the se estimated in the first place. Normally they should not different so much, but might have to do with your model and how the errors are estimated.