Does confounding always imply endogeneity?

Question

I'm a bit confused with the definitions regarding causal inference. My question is whether we can call measured confounding an endogeneity problem?

Answer 1

I would say no. Confounding per se could be endogenous, or it might not be. But if the confounding variable is measured, then it's no longer endogeneity. Here's an example of endogenous confounding:

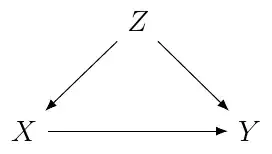
Here $U_Y$ is an exogenous variable that we will assume gives rise to the error term for $Y.$ $X$ is confounded with $U_Y,$ which is the definition of endogeneity. Typically, $U_Y$ is not measured. But you could have a similar-looking but quite different situation here:

Now $Z$ is a measured variable, and is a confounder for the effect of $X$ on $Y,$ the same as before, except that $Z$ is measured. Once the confounding variable is measured, you no longer include it in the error term; and once you no longer include a variable in the error term, it ceases being endogeneity.