I am trying to fit a mixed model in lme4 using the lmer.
the model form is:
model<- lmer(entropy ~ X1 * X2 + (1| video) + (1| subject), REML = FALSE
entropy is a continuous variable but normalised now between 0 and 1.
X1 is a centred and scaled continuous predictor, and X2 is a categorical predictor with 4 levels. I should note that entropy was computed from a variable that had a too many zeros, and so, during the normalisation of the variable I had to add a very small number number to avoid undefined logarithms. As a result, the distribution of entropy is somewhat bimodal:
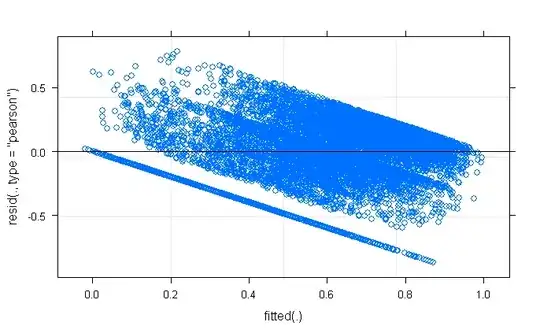
I am aware that the distribution of the outcome does not matter for the assumptions of linear models (whereas the residuals distribution do). However, the residual plot for this model shows a decreasing trend which I am worried about.
I am not quite sure what to make of this pattern, or how to improve this model. I initially fitted this using lmer, tried log-transforming and it didn't help. when I extract and compute the actual correlation between the fitted and residuals it is actually close to zero, which is puzzling considering this trend.
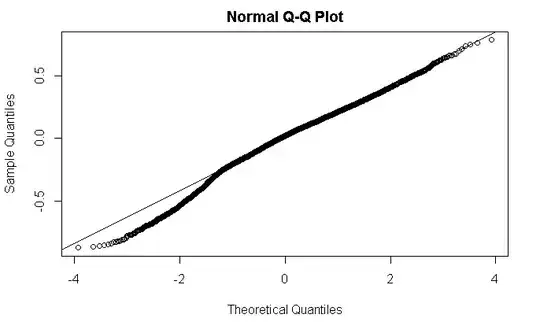
the qq-norm plot doesn't look terrible
qqnorm(resid(model)
Histograms of the residuals look pretty normal, but I am aware histograms are not appropriate to check for the random distribution of residuals assumption of linear models.
I tried including other predictors that are of interest as well as running a few glmer (e.g. binonimal) models but I can't seem to resolve this.
Any suggestions on how to remedy this? How worried should I be about the first residual plot above?
Thanks, any suggestions are very much appreciated!