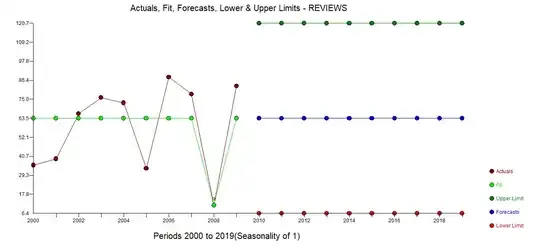
I have following data from product reviews that were recoreded yearly. The higher the score, the better it is.
year 2000, 2001, 2002, 2003, 2004, 2005, 2006, 2007, 2008, 2009
score 35.3, 39,1, 66.3, 75.9, 72.8, 33.3, 88.2, 78.1, 11.2, 82.8
Now I want to get overall score to understand how good this product was over the years.
When I use mean it gives equal weight to all the years. However, I want to get the overall score by weighting more on the recent years. Therefore, I used the following equation.
overall_score = (0.1(score_of_2000) + 0.2(score_of_2001) + 0.3(score_of_2002) + 0.4(score_of_2003) + 0.5(score_of_2004) + 0.6(score_of_2005) + 0.7(score_of_2006) + 0.8(score_of_2007) + 0.9(score_of_2008) + 1.0(score_of_2009) + 0.1(score_of_2010)) /10
However, this is like linearly weighting the years. Is there a better way of favouring more recent years?
I am happy to provide more details if needed.