2

I have a question relative to the correct method to deal with univariate outliers when one has to conduct an ANOVA.

Starting with an example, suppose I have two samples of subjects tested on a number of dependent variables. For each dependent variable I run an ANOVA with group as independent variable. Suppose, now, that I have identified a series of univariate outliers for each dependent variable.

Have I to first remove all the outliers and then conduct the various ANOVAs, or have I to remove only the outliers relative to the specific dependent variable for which I'm conducting the ANOVA?

chl
  • 50,972
  • 18
  • 205
  • 364
this.is.not.a.nick
  • 862
  • 2
  • 13
  • 25

1 Answers1

3

"I refer to outliers identified by the boxplot"

You can miss many outliers proceeding this way: an observation can be outlying in the multivariate (design,dependant)-space without being obviously outlying in any of the (design/dependant) variable taken in isolation.

The best procedure is simply to use an estimation method that is not affected by outliers. Robust anova/regression routines are implemented in most common statistical software. As an example in R in the package robustbase.

Below I illustrate how multivariate outliers can wreck a linear model without standing out in any of the (design/dependant) variable individually.

library(robustbase)
data(salinity)
library(MASS)

Xa<-mvrnorm(5,colMeans(salinity[,paste0("X",1:3)]),cov(salinity[,paste0("X",1:3)]))
Ya<-Xa%*%c(-2,0,2)+rnorm(5,0,1/5)-20
salinity2<-as.data.frame(cbind(c(salinity$X1,Xa[,1]),c(salinity$X2,Xa[,2]),c(salinity$X3,Xa[,3]),c(salinity$Y,Ya)))
colnames(salinity2)<-colnames(salinity)

By construction, these 5 outliers will not visible on the variable-wise boxplots.

variable-wise boxplots

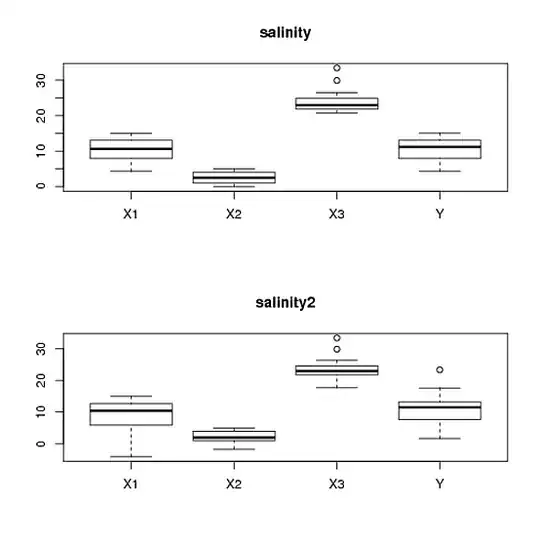
Yet, if you run an ANOVA on salinity2 you will get completely different results as an ANOVA ran on salinity. The robust ANOVA on the other hand gives essentially the same results for salinity2 as for salinity:

m0r.sali<-lmrob(Y~.,data=salinity)
m0c.sali<-lm(Y~.,data=salinity)

m1r.sali<-lmrob(Y~.,data=salinity2)
m1c.sali<-lm(Y~.,data=salinity2)

summary(m1r.sali)$coef
summary(m0r.sali)$coef

summary(m1c.sali)$coef
summary(m0c.sali)$coef

Here is a good recent review article on robust statistics.

user603
  • 21,225
  • 3
  • 71
  • 135
  • 2
    Yes. The bottom line is that ANOVA deals very poorly with many non-normal distributions, whether this is in the form of outliers from an otherwise Normal distribution or of a skewed distribution. Particularly in the small sample sizes that are common in certain fields. Modern robust methods are a must. – Peter Ellis Dec 16 '12 at 00:39
  • Thanks for your clarity and for the example. From your answer, can I conclude that in your opinion removing outliers is not a good practice? Anyway, I considered univariate outliers since I had to run single ANOVAs, so taking one dependent variable at once. I would have considered multivariate outliers if I had to conduct a MANOVA for all the dependent variables. Is this line of reasoning correct? – this.is.not.a.nick Dec 16 '12 at 08:52
  • 1
    no and no. I showed an example with a single dependent variable and 3 design variables. I showed that even in this simple case, it is possible for harmful outliers to remain hidden on boxplots of the variables. Therefore, using variable-wise boxplots to identify outliers is not sufficient. Robust methods start by identifying the outliers and then down-weight them. Using a robust method on the original sample is essentially the same as finding the outliers and using a non robust method on the cleaned data. – user603 Dec 16 '12 at 10:28