0

I have a statistical sample where D10 = 8 (10% of population under the value 8), D50 = 11 (median), and D90 = 18 (90% of population under the value 18)

Now, I need to find the best fit, in terms of the values $\mu$ and $\sigma^2$ of a lognormal probability distribution, given these D values.

Any help is highly appreciated

Oier Arcelus
  • 1
  • 1
    The likelihood is equal to the joint density of the order statistics $D10, D50, D90$. This density has a closed form formula, see https://en.wikipedia.org/wiki/Order_statistic#The_joint_distribution_of_the_order_statistics_of_an_absolutely_continuous_distribution. This can in turn be maximised numerically with respect to $\mu$ and $\sigma^2$. See https://stats.stackexchange.com/a/436621/77222 for a similar approach – Jarle Tufto Apr 09 '20 at 09:31
  • But isn't the CLT that you use to derive the mean, only true when the sample size is large? – Oier Arcelus Apr 09 '20 at 09:48
  • 1
    You'll need to use the joint density of your three order statistics (D10, D50 and D90). The distribution of the sample mean isn't needed. – Jarle Tufto Apr 09 '20 at 09:51
  • Ok, one more question, why do you need to use a truncated lognormal based on x1 and xn? I though x1 and xn were the sample max and min, not the max and min of the actual distribution. In my case I can have 10% of samples that are lower than 8 and larger than 18. – Oier Arcelus Apr 09 '20 at 10:26
  • That's specific to the other question and doesn't apply here. – Jarle Tufto Apr 09 '20 at 10:32
  • I solved it, I think, thanks! – Oier Arcelus Apr 09 '20 at 14:11

1 Answers1

0

Followin the suggestions of Jarle Tufto.

I coded the following.

 import numpy as np 
 import matplotlib.pyplot as plt
 from scipy import special
 from scipy import optimize  

 osample = [8,11,18] #ordered D10, D50, D90 sample
 num = 3

 def lnpdf(x,mu,sigma): #lognormal probability distribution function
     d = 1/(x*sigma*np.sqrt(2*np.pi))*np.exp(-0.5*(np.log(x) - mu)**2/sigma**2)
     return d

 def jpdfo(mu,sigma): #joint probability distributions of ordered statistic
     p = 1
     for i in osample:
         p *= lnpdf(i,mu,sigma)
         p = np.math.factorial(num)*p
     return p

 def nll(param): # negative log likelihood
     val = -jpdfo(param[0],param[1])
     return val

 #minimize the nll
 x0 = [10,3]
 res = optimize.minimize(nll,x0=init,method="Nelder-Mead")
 print(res)

What I obtain is the following:

final_simplex: (array([[2.45588837, 0.33356707],
   [2.45592186, 0.33361764],
   [2.45597456, 0.33356375]]), array([-0.00144556, -0.00144556, -0.00144556]))
       fun: -0.001445562771159583
   message: 'Optimization terminated successfully.'
      nfev: 95
       nit: 49
    status: 0
   success: True
         x: array([2.45588837, 0.33356707])

So judging from this $\mu$ = 2.45 and $\sigma$ = 0.33. If I plot a lognormal distribution with these parameters, I obtain the following:

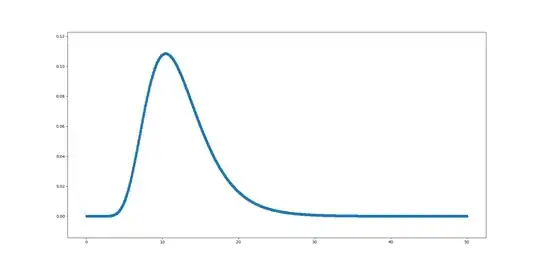
enter image description here

Which pretty much makes sense, given my sample data. I will call this good for now, thanks Jarle!

Oier Arcelus
  • 1