6

I have a dataset with several hundred pH measurements from a factory line. This dataset will be used to infer process capability using Minitab.

On a physical basis, pH is a continuous scale (being the negative logarithm of the concentration of free hydrogen ions in solution). However, due to the resolution of the measuring instrument (reads out to 0.01) and relatively narrow range of values (min: 3.34, max: 3.74), there is a limited number of discrete values the measurement can take.

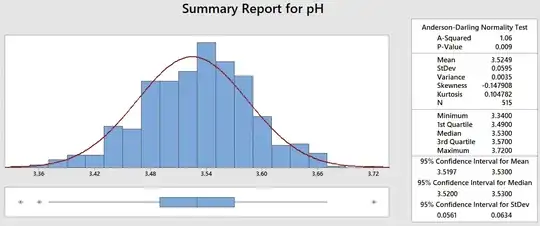
Looking at the data it indeed appears to be normal, however the Anderson-Darling test gives a p-value of <0.05, indicating non-normal data:

histogram of pH values

percentile plot of pH values

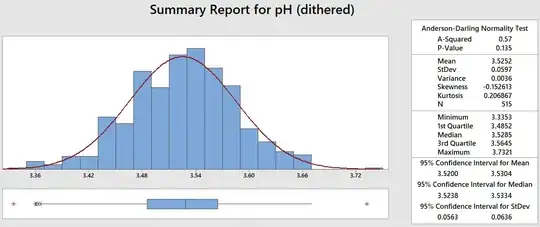
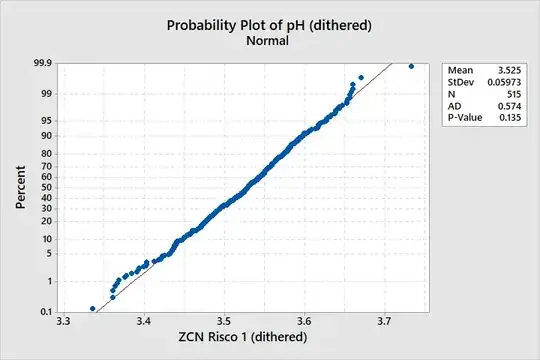
If I dither the data using "small-compared-to-process-variation" normally distributed noise ($\mu$ = 0, $\sigma$ = 0.005) the distribution does not change in any meaningful way. The relevant population parameters and/or visually). However, the A-D test gives a much higher p-value, indicating normality of the data:

histogram of dithered pH values

percentile plot of dithered pH values

Coming from a Six Sigma Green Belt background, where normality is king & molesting the data is strictly verboten, this feels like a conundrum. I would like to use that dataset to estimate process capability, however Minitab warns me about the non-normality (and so would my former 6σ coach).

My question therefore is two-fold:
1) Can I use the raw (non-dithered) data to infer process capability?
2) Is dithering needed and/or a valid way to pre-process the data prior to capability analysis?

Markos Strofyllas
  • 63
  • 4
  • 1
    As with all things, "it depends" is probably the place to start, but the data on the probability plots looks like it passes The Fat Finger (or Fat Pencil) test. If you are required to have a justification for using the Normality assumption in the capability analysis, then use the Ryan-Joiner normality test. It deals with rounding/ties whereas AD doesn't. Minitab has a blog on this: https://blog.minitab.com/blog/the-statistical-mentor/normality-tests-and-rounding – MichiganWater May 26 '20 at 06:21

1 Answers1

9

When you have many observations like the hundreds that you have, a goodness-of-fit test is going to pick up on subtle deviations that are unlikely to interest you.

You’re right: because of the discreteness of the measurements,$^{\dagger}$ your data cannot be normal, and your test is confirming that your data are not from a normal distribution.

But you already knew that.

The general sentiment on Cross Validated is that this type of testing is not that helpful. Either you lack the sample size to have adequate power to detect an interesting difference, or your test is overpowered and will detect differences that aren’t interesting.

Your plots, especially the quantile-quantile plot, are evidence to me that your data are normal enough for pretty much any purpose.

$^{\dagger}$ There may be other reasons. I was going to say that your values are bounded, but pH doesn’t have to fall between 0 and 14 like they told me in middle school, I’ve learned.

Dave
  • 28,473
  • 4
  • 52
  • 104
  • Much appreciated! Regarding the "other reasons" footnote: pH is a logarithmic scale, therefore I would expect $10^{pH}$ to be normally distributed. However, given the narrow range of the process as well as other mitigating factors (predominantly buffering capacity of the product), the first-order approximation of normality for pH should work Well Enough For Our Purposes™ – Markos Strofyllas Apr 07 '20 at 16:48
  • One follow-up question: can you suggest sources for your "because of the discreteness of the measurements, your data cannot be normal" remark? I asked the same question when I took the Six Sigma course but the instructor gave a vague, non-committal response and moved on, so I still have the itch to understand why. – Markos Strofyllas Apr 07 '20 at 16:56
  • pH is approximately normal, so raising it to a power of 10 will produce an approximately lognormal distribution. – Nick Cox Apr 07 '20 at 17:00
  • 1
    @MarkosStrofyllas A normal distribution is continuous, so if your distribution is discrete, it simply cannot be truly normal. However, you’re so close to normal that you, probably, can proceed as if you had true normality. – Dave Apr 07 '20 at 17:02
  • 1
    @MarkosStrofyllas : Regarding non-normality: Turn your head 45 degrees to the left and look at your discretized data quantile plot. Your data see-saws back and forth across the normality line (near the mean), giving many points "far" from the line. Now do the same thing to your dithered data and notice that the data conforms **much** more closely to the line (near the mean). Actually normally distributed data (with so many samples) conforms very closely to the line near the mean. – Eric Towers Apr 08 '20 at 03:05
  • @Eric Towers thanks for the visual explanation, that did the trick for me! – Markos Strofyllas Apr 08 '20 at 10:40