3

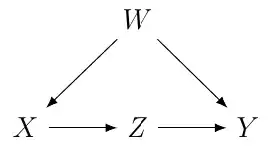
Pearl et al. "Causal Inference in Statistics: A Primer" (2016) p. 39 states the following:

Rule 1 (Conditional Independence in Chains) Two variables, $X$ and $Y$, are conditionally independent given $Z$, if there is only one unidirectional path between $X$ and $Y$ and $Z$ is any set of variables that intercepts that path.

(And then notes that the rule only holds if the error terms associated with the variables are independent of each other.)

As a non-native speaker, I am not entirely sure I understand the rule correctly. Does the if clause say that

  1. there can only be one path AND
  2. that path must be unidirectional?

Or does it say that

  1. there can be many paths, but
  2. among them only a single one is unidirectional?

Or ...? (My understanding of the English punctuation suggests the second alternative, but my understanding of the context points to the first one.)

Adrian Keister
  • 3,664
  • 5
  • 18
  • 35
Richard Hardy
  • 54,375
  • 10
  • 95
  • 219

2 Answers2

3

I think Pearl is a bit ambiguous. (Thanks to eric_kernfeld for improving my understanding.) From the point-of-view of normal English usage, it is the second understanding. The adjective "unidirectional" modifies the first occurrence of the word "path", making up a single term: unidirectional path. The "if" part says there is only one of those. To say the first, you would have to word it like this:

... if there is only one path, unidirectional, such that...

or

... if there is only one path, that path is unidirectional, and ...

On the other hand, this DAG shows that $X$ and $Y$ can be dependent, even if $Z$ satisfies the second interpretation. Here, $X$ and $Y$ are not independent conditional on $Z,$ even though $Z$ satisfies the second interpretation.

enter image description here

In context, the first interpretation makes more sense.

Community
  • 1
Adrian Keister
  • 3,664
  • 5
  • 18
  • 35
  • Interestingly, a previous answer (now deleted) said *Your first understanding is correct. You can generalize Rule 1 to multiple unidirectional paths, as long as the variables in Z intercept all of those paths (and error terms are orthogonal)*. Now a quick follow-up question: why cannot there be many unidirectional paths where $Z$ would intercept each of them? This would be a less restrictive definition. Is the latter not restrictive enough so that only the definition as given is valid? (I can later post it separately if you have an answer so that you earn all the points you deserve.) – Richard Hardy Apr 14 '20 at 18:59
  • @eric_kernfeld, could you please elaborate? – Richard Hardy Apr 14 '20 at 19:01
  • Reposting my deleted comment: it said "The rule doesn't say if and only if". – eric_kernfeld Apr 14 '20 at 19:02
  • @eric_kernfeld I'm not sure that matters in this context. – Adrian Keister Apr 14 '20 at 19:03
  • @RichardHardy I think in the spirit of the Rule, that would likely also be sufficient conditions for conditional independence. – Adrian Keister Apr 14 '20 at 19:04
  • I deleted my comment because I'm not sure whether this is being used as a definition or whether it is a lemma to be proved from the customary definition (P(A,B|C) = P(A|C) P(B|C)). I assume the latter, so in my comment, I meant that this is not presented as an equivalent condition: if viewed as a lemma rather than a definition, it does not claim to capture all cases of conditional independence. – eric_kernfeld Apr 14 '20 at 19:04
  • Yes, I am also not clear as to whether a "Rule" in Pearl's language, is a definition or a lemma. I'm not at all sure that his version of 'conditional independence in chains' is the same thing as 'conditional independence' - in probability. I'm sure you're right that this Rule does not capture all cases of conditional independence. – Adrian Keister Apr 14 '20 at 19:13
  • This answer would make sense on the English language SE, but on the stats SE, it's clearly wrong. Judea Pearl uses the same probability theory as everyone else, and the second understanding is wrong whether this "rule" is a definition meant to capture all cases, or a lemma meant to check only some of them. See my example. – eric_kernfeld Apr 14 '20 at 19:49
  • Then I would argue Pearl needs to clarify this rule, because it's not clear. – Adrian Keister Apr 14 '20 at 20:03
  • Let us [continue this discussion in chat](https://chat.stackexchange.com/rooms/106747/discussion-between-eric-kernfeld-and-adrian-keister). – eric_kernfeld Apr 15 '20 at 15:11
  • In the new version of this answer, you write "Here, and are not conditionally independent of ". I think a better wording would be " and are not independent conditional on ". – eric_kernfeld Apr 15 '20 at 15:14
  • Adrian, so what is you current best guess? Is it the first interpretation? – Richard Hardy Apr 15 '20 at 16:59
  • Yeah, I would have to say, in context, that it's the first interpretation. That fits better with the word "chain", anyway, which is something like $X\to Z\to Y.$ – Adrian Keister Apr 15 '20 at 17:00
1

Here's an example that casts doubt on your second interpretation, but is compatible with the first one. Consider the following R code.

a = runif()
b1 = a + runif()
b2 = a + runif()
c1 = b1 + runif()
c2 = b2 + runif()
d = c1 + c2 + runif()

This corresponds to the following DAG. 

a  -> b1 -> c1 
↓           ↓
b2 -> c2 -> d

Suppose we are assessing the independence of A and C1 conditional on {B1,D} as claimed by this lemma or definition. By the second understanding, the criterion is satisfied: there is only one unidirectional path, a->b1->c1, and it is interrupted. By the first understanding, the criterion is not satisfied, because there exists another path a-> b2 -> c2-> d<-c1 (though it is not unidirectional).

Suppose D is 0.1 for this whole example. If C1 is also 0.1, then A must be 0, because $0=D-C_1=C_2\geq A \geq 0$. Under smaller values of C1, A may be as large as 0.1. So in terms of probability theory, A and C1 are not independent conditional on D. Thus, either the lemma describes a concept of conditional independence that is distinct from that typically used in probability theory, or (more likely) the first understanding, not the second, is what Pearl meant -- though you're right that the wording matches the second better.

eric_kernfeld
  • 4,828
  • 1
  • 16
  • 41
  • I may need to modify the details of this little example, because my initial idea incorrectly asserted that 0 and 0 are not independent. Clearly they are. I think the same DAG will work somehow though. – eric_kernfeld Apr 14 '20 at 19:35
  • Right, conditioning on $D$ opens up the collider. You could coalesce $B_2$ and $C_2$ to simplify a bit. – Adrian Keister Apr 14 '20 at 20:04
  • Another couple of related threads (in case you had time for them): ["Adjustment formula for counterfactuals: can we get rid of $X=x$?"](https://stats.stackexchange.com/questions/460338/) and ["Law of total probability and conditioning on multiple events"](https://stats.stackexchange.com/questions/458936/) (just to confirm/disconfirm the existing answer). – Richard Hardy Apr 15 '20 at 17:30