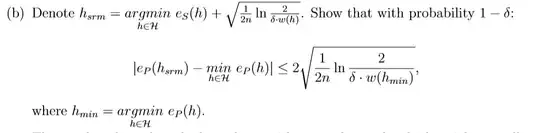tl;dr:
The main question is if I use an inequality that is true with a certain probability (confidence) twice, do I get the same confidence?
Original:
I've got the following exercise:
Where $e_p(h)$ denotes the true 0-1 loss of the hypothesis $h$ over the true distribution $P$, and where the labels/outputs are binary $\in \{0,1\}$.
Now, from (a) I've got that $e_p(h) \le e_s(h) +\sqrt{\frac{1}{2n}\ln\frac{2}{\delta w(h)}}$, and $e_s(h) \le e_p(h) +\sqrt{\frac{1}{2n}\ln\frac{2}{\delta w(h)}}$ where $e_s(h)$ is the sample (average) error. This was derived using Hoeffding's inequality, and is true with confidence $1-\delta$.
Now, to solve (b), I used the following:
$e_p(h_{srm}) - e_p(h^*) \le e_s(h_{srm}) + \sqrt{\frac{1}{2n}\ln\frac{2}{\delta w(h_{srm})}} - e_p(h^*) \\ \le e_s(h^*) + \sqrt{\frac{1}{2n}\ln\frac{2}{\delta w(h^*)}} - e_p(h^*) \le 2\sqrt{\frac{1}{2n}\ln\frac{2}{\delta w(h^*)}}$
I used (a) in the first move, definition of SRM in the 2nd, and then (a) again.
The problem, and my question is, if I used Hoeffding's inequality twice for two distinct hypothesis, doesn't it mean my confidence is no longer $1-\delta$ but rather $(1-\delta)^2$ ?