How to construct this "prediction heatmap" assuming OLS (worked out example)

Question

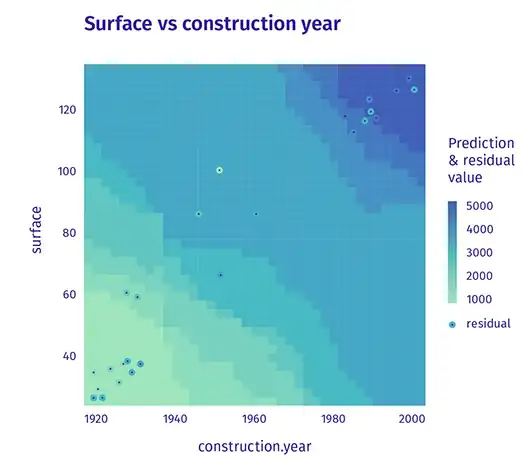
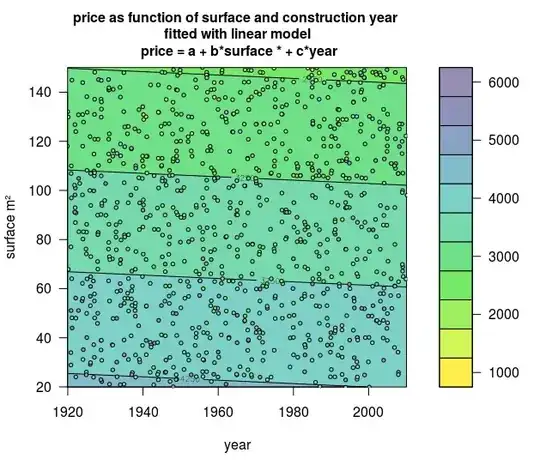
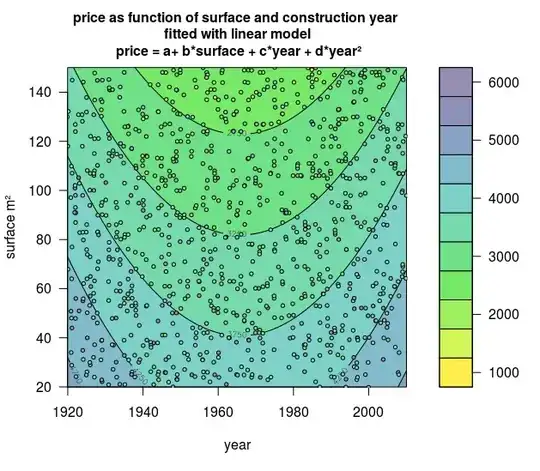
The following visual certainly delivers in terms of eye candy:

There was no details on the model specification, but let's just assume its something like:

$$price = \beta_{0} + \beta_{1} x_{surface} + \beta_{2} x_{cyear} + \epsilon$$

Where:

• $price$ - the selling price of a house
• $x_{surface}$ - the surface area of the house
• $x_{cyear}$ - the year the house was constructed

Edit

After much effort, I found a way to iterate through the domain of the variables age and area using coefficients to get prediction values. I left out residuals for simplicity. Here is my code:

c = 20595
area = 39.28
age = -402.5
master_array = []
step = 50
x_range = 3800
y_range = 50
for i in range(step):
    for j in range(step):
        temp = {}
        temp['x'] = i*(x_range/step)
        temp['y'] = j*(y_range/step)
        temp['pred'] = c+((i*x_range/step)*area+(j*y_range/step)*age)
        master_array.append(temp)

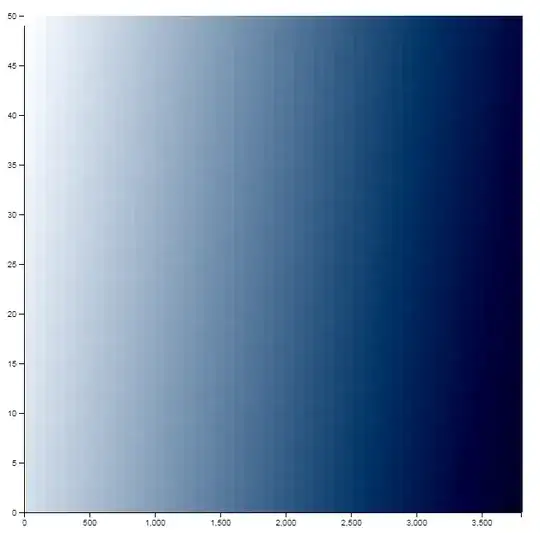
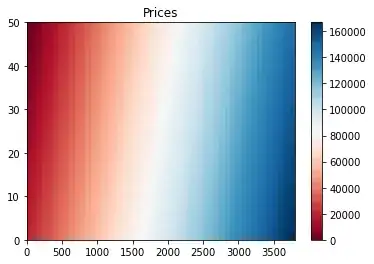
I have made modest progress. The constant and coefficients age and area I obtained after I ran a regression using the above specification on a data set from my econometrics text book. Clearly, the output should not be expected to be exactly the same as the inspiration visual, but I didn't get anywhere near the spread of prediction regions. Mine looks simply like a gradient. Output below, age is y axis, area is x axis, light blue=cheap house, dark blue= expensive house:

I'm concerned there is a flaw in my code. Quick inspection led me to notice there appears to be no negative relationship of age shown in the plot (we would expect more darker blue regions where age is close to 0. Maybe someone with experience with this type of visual can advise on my implementation.

Question

Can we expect OLS estimation to only have a 'boring' linear gradient for prediction regions, as seen in my visual, or maybe it's user error on my part? Either way, what type of estimation could explain the 'cool' / 'interesting' prediction zones seen in the inspiration visual?

Answer 1

There is probably nothing wrong with your code, but it's hard to tell as it is not complete and reproducible.

Age has a much smaller influence on the price than area: For the largest house, the price, if it were new, would be around 170,000. If it were 50 years old, the price would still be around 150,000. You can see it better if you use a diverging color map:

This image was generated by the following code:

import numpy as np
import matplotlib.pyplot as plt
c       = 20595.
area    =    39.28
age     =  -402.5
step    =    50
x_range =  3800
y_range =    50
dy, dx = y_range/step, x_range/step

x, y = np.mgrid[slice(0, x_range + dx, dx),
                slice(0, y_range + dy, dy)]
z = c + x*area + y*age
z = z[:-1, :-1]
z_min, z_max = 0, np.abs(z).max()

fig, ax = plt.subplots()
qm = ax.pcolormesh(x, y, z, cmap='RdBu', vmin=z_min, vmax=z_max)
ax.set_title('Prices')
fig.colorbar(qm, ax=ax)
plt.show()

Answer:

As long as your predictor terms are all linear, the boundary is bound to be "boring". If you want an "interesting" boundary, you need to introduce non-linearities, like

z = 1e5*(np.sin(2*x/x_range) + np.cos(2*y/y_range)+1)**2
z = z[:-1, :-1]
z_min, z_max = 0, np.abs(z).max()

fig, ax = plt.subplots()
qm = ax.pcolormesh(x, y, z, cmap='RdBu', vmin=z_min, vmax=z_max)
ax.set_title('Prices')
fig.colorbar(qm, ax=ax)
plt.show()

The image you quote in your question likely depicts the prediction by a non-linear model, perhaps random forest or neural network.

Answer 2

I'm concerned there is a flaw in my code. Quick inspection led me to notice there appears to be no negative relationship of age shown in the plot (we would expect more darker blue regions where age is close to 0. Maybe someone with experience with this type of visual can advise on my implementation.

About the true relationship:

In the answer below I assume that your question relates to the apartments dataset from the DALEX package. Your dataset might be slightly different, but I guess that it will still work

You are right that there is not much influence from the age when you fit with only a linear term.

Note that the dataset is specifically generated to relate to the effect of Anscombe's quartet (It is artificial data).

From the R documentation for the DALEX package:

Structure of the dataset is copied from real dataset from PBImisc package, but they were generated in a way to mimic effect of Anscombe quartet for complex black box models.

And the true relation is:

$$\begin{array}{rcl} \text{price} &=& 5000 + 600 \cdot \underbrace{(\vert \text{year}-1965 \vert > 30)}_{\llap{\text{this is a logical variable}}\rlap{\text{ with values 0 or 1}}} \\ && - 10 \cdot \text{surface} - 100 \cdot \text{floor} - 50 \cdot n_{\text{rooms}} + 1.5 \cdot \text{district} \end{array}$$

So, while there is nearly zero correlation between price and age, there is still some some sort of quadratic relationship between price and age.

When you fit a linear model with only a linear term for age then the coefficient will be close to zero. But with a quadratic term for age you should get some curved function.

Examples of fits with different models

Linear models

$$\mathbf{\text{price} = a + b \cdot \text{surface} + c \cdot \text{year}}$$

$$\mathbf{\text{price} = a + b \cdot \text{surface} + c \cdot \text{year} + d \cdot \text{year}^2}$$

$$\mathbf{\text{price} = a + b \cdot \text{surface} + c \cdot (\vert\text{year} - 1965\vert > 30)}$$

Random forest model:

Support Vector Regression

Answer 3

As I mentioned in a comment above, it is hard to understand what you want. If you want diverging confidence intervals, see code below.

import numpy as np
import pandas as pd
import seaborn as sns
from matplotlib import pyplot as plt

plt.close('all')
x = [t for t in np.linspace(0, 5,num=20)]
x.append(22)
x.append(-11)
x = np.array(x)
alpha, beta = 223, 2.34
y = alpha + beta*x + np.random.normal(loc=0,scale=0.4, size=x.shape)
y[-2] = y[-2] - 15
y[-1] = y[-1] - 25
df = pd.DataFrame(data=np.vstack([x,y]).T, columns=['x', 'y'])
sns.regplot(
    x='x',
    y='y',
    data=df)
plt.show()

The blue line is calculated using OLS. Confidence intervals are drawn using bootstrap - sampling the data with replacement and fitting a line on sampled data using OLS.