4

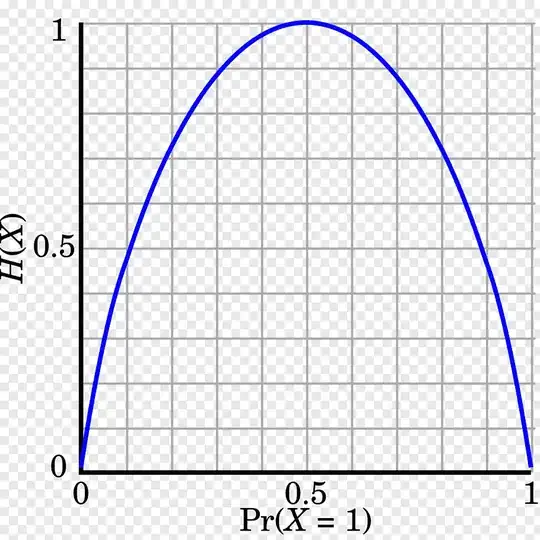
The notion of information as per Shannon is that if the probability of RV is close to 1, there is little information in that RV because we are more certain about the outcome of the RV so there is little information that RV can provide us.

Contrasting this to Fisher information which is the inverse of the covariance matrix, so by that definition if the variance is high meaning the uncertainty is high we have little information and when uncertainty is low (probability of RV close to 1) the information is high.

The two notion of information is conflicting and I would like to know if I understood it wrong?

From one of the references provided by @doubllle the following plot shows what Shannon entropy is for the coin flip model parametrized by $\theta$ of Bernoulli distribution Vs the same for Fisher information

Shannon Entropy

enter image description here

GENIVI-LEARNER
  • 720
  • 4
  • 13
  • 2
    Cramer Rao theorem states that the inverse of Fisher Information is **bounded** by the cov matrix. And Fisher Information is defined for the carried information in $X$ about parameter $\theta$. When the uncertainty is low (the observations not wide spreaded), naturally we are more certain about $\theta$. See [here](https://arxiv.org/pdf/1705.01064.pdf) and [here](https://web.stanford.edu/class/stats311/Lectures/lec-09.pdf) – doubllle Mar 31 '20 at 21:06
  • good references, I shall look at them and revert back. So essentially when I mentioned about Fisher information in my question is wrong? I am struggling to relate Shannon's notion of information with Fisher information. – GENIVI-LEARNER Apr 01 '20 at 15:51
  • If I were you, I'd rephrase the second paragraph. Please also check this: https://stats.stackexchange.com/questions/196576/what-kind-of-information-is-fisher-information/197471#197471 Your question is somehow covered there – doubllle Apr 01 '20 at 20:40
  • @doubllle thats a lot for the effort. Your references are really "informative" pun intended :) Will take some time for me to crunch them. – GENIVI-LEARNER Apr 02 '20 at 16:05

2 Answers2

4

Fisher information and Shannon/Jaynes entropy is very different. For a start, the entropy $\DeclareMathOperator{\E}{\mathbb{E}} H(X) =-\E \log f(X)$ (using this expression to have a common definition for continuous/discrete case ...) showing the entropy is the expected negative loglik. This only relates to the distribution of the single random variable $X$, there is no necessity for $X$ to be embedded in some parametric family. This is in a sense the expected informational value from observing $X$, calculated before the experiment. See Statistical interpretation of Maximum Entropy Distribution.

Fisher information, on the other hand, is only defined for a parametric family of distributions. Suppose the family $f(x; \theta)$ for $\theta\in\Theta \subseteq \mathbb{R}^n$. Say $X \sim f(x; \theta_0)$. Then the fisher information is $\DeclareMathOperator{\V}{\mathbb{V}} \mathbb{I}_{\theta_0} = \V S(\theta_0)$ where $S$ is the score function $S(\theta)=\frac{\partial}{\partial \theta} \log f(x;\theta)$. So the Fisher information is the expected gradient of the log likelihood. The intuition being that where the variance of the gradient of the loglik is "large", it will be easier to discriminate between neighboring parameter values. See What kind of information is Fisher information?. It is not clear that we should expect any relationship between these quantities, and I do not know of any. They are also used for different purposes. The entropy could be used for design of experiments (maxent), Fisher information for parameter estimation. If there are relationships, maybe look at examples where both can be used?

kjetil b halvorsen
  • 63,378
  • 26
  • 142
  • 467
  • Qutie comprehensive answer. I didnot understand what you meant by `where the gradient of the loglik is "large", it will be easier to discriminate between neighboring parameter values` Why shall it be easier to discriminate between neighboring parameter values? and what exactly is "discriminate"? – GENIVI-LEARNER Apr 05 '20 at 12:39
  • See the edit, was missing "variance of". Estimating by maximum likelihood, we search where the gradient is zero, if the gradient is varying more with the data, the maximum will be more precisely located. See the linked post. – kjetil b halvorsen Apr 06 '20 at 18:50
  • ok it makes sense. So second derivative measures how fast the gradient is varying, right? – GENIVI-LEARNER Apr 06 '20 at 21:11
1

They are both information but are informing you about different things. Fisher information is related to estimating the value of a parameter $\theta$:

$$I_\theta = {E}\left [ \nabla_\theta \log p_\theta(X)\nabla_\theta \log p_\theta(X)^T \right ] $$

What Fisher information is measuring is the variability of the gradient for a given score function, $\nabla_\theta \log p_\theta(X)$. An easy way to think about this is if the score function gradient is high, we can expect that the variability of the score function is high and estimation of the parameter $\theta$ is easier.

Shannon information is related to the probability distribution of possible outcomes. In your coin example there is little information from a probability distribution in the extreme cases, $P(X = 0)$ and $P(X = 1)$. If you knew the probability distribution you would not be surprised or uncertain about any observation at these cases. The higher entropy at $P(X = 0.5)$ produces the maximum uncertainty.

dtg67
  • 101
  • 4
  • I am just little confused. So take the coin example. Shannon information measures the information we will get "after" the coin is tossed keeping the parameter constant while Fisher information determines the information of the variability of the parameters itself so maybe the variance in parameter for biased coin could be 0.6,0.65,0.7 etc so does Fisher information measure that? – GENIVI-LEARNER Apr 02 '20 at 18:44
  • 1
    Fisher information requires observations of a random variable and then models that distribution using a parameter $\theta$. In Shannon information there is no parameter because it's not modeling a distribution given an observation of random variables. Shannon is measuring the uncertainty of a given process. This is why we have zero uncertainty of what coin side will be observed at the extremes in the coin example and maximum uncertainty when both sides are equally likely. – dtg67 Apr 02 '20 at 19:45
  • Well in that case in Shannon's entropy, the information pertains to uncertainty? So high uncertainty, the high information we will obtain once the outcome is observed. Well that makes sense. And in Fisher scenario the concept of information is how much the score function varies? – GENIVI-LEARNER Apr 02 '20 at 20:06
  • Also why do you say `variability of the score function is high and estimation of the parameter is easier`. what does high variability of score function got to do with estimation of parameter being easier? So if the variability is low the parameter estimation is difficult? – GENIVI-LEARNER Apr 02 '20 at 20:09