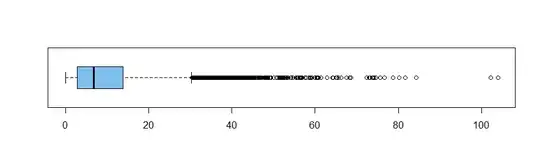
Taking a large (n >> 10 000) data set where the population is clearly not normal and detecting/testing for outliers using mean +/- 3 standard deviations.
Multiple colleagues of mine use this approach to detect outliers. I'm arguing that this is wrong and multiple sources state normality needs to be fulfilled otherwise the tests are inaccurate, but what is it that makes the above test inaccurate?
Additionally, if someone uses the above tests on a non-normal data and finds X outliers, can you draw any conclusions or is the only conclusions "the data set had X outliers, however, the data was not normal and therefore the test was inaccurate"?