difference in standard errors between 2 seemingly equivalent models

Question

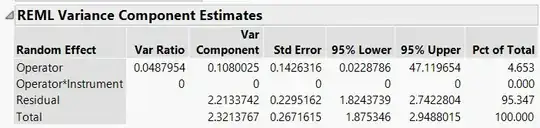
Consider a crossed design with 3 operators and 4 instruments. Interest is in the instrument effect.

Could you explain me the difference in standard errors of the fixed effects between the two seemingly equivalent models below?

Model 1

fixed effect: instrument
random effect: operator, operator*instrument

Model 2

fixed effect: instrument
random effect: operator*instrument

Here is the data is

Operator    Part    Instrument  new Y
Janet   1   1   9.110079
Janet   1   2   8.142277
Janet   1   3   11.26354
Janet   1   4   9.919439
Janet   2   1   11.74011
Janet   2   2   8.377658
Janet   2   3   9.942735
Janet   2   4   10.40425
Janet   3   1   10.20466
Janet   3   2   8.379429
Janet   3   3   12.22024
Janet   3   4   12.61237
Janet   4   1   8.807384
Janet   4   2   8.030572
Janet   4   3   13.08309
Janet   4   4   10.01584
Janet   5   1   8.099196
Janet   5   2   8.364157
Janet   5   3   13.41016
Janet   5   4   14.76918
Janet   6   1   8.106056
Janet   6   2   8.10354
Janet   6   3   8.482492
Janet   6   4   8.154287
Janet   7   1   7.111584
Janet   7   2   7.903323
Janet   7   3   6.939069
Janet   7   4   5.344401
Janet   8   1   7.485183
Janet   8   2   7.817825
Janet   8   3   6.845474
Janet   8   4   6.899052
Bob 1   1   8.23373
Bob 1   2   8.057511
Bob 1   3   9.661005
Bob 1   4   8.094992
Bob 2   1   8.087004
Bob 2   2   8.088673
Bob 2   3   8.220318
Bob 2   4   9.147579
Bob 3   1   8.864142
Bob 3   2   8.061816
Bob 3   3   8.925117
Bob 3   4   8.976143
Bob 4   1   8.056059
Bob 4   2   8.084911
Bob 4   3   8.348538
Bob 4   4   8.548607
Bob 5   1   8.069039
Bob 5   2   8.007888
Bob 5   3   9.626642
Bob 5   4   9.733307
Bob 6   1   8.024802
Bob 6   2   8.005744
Bob 6   3   8.434947
Bob 6   4   8.453447
Bob 7   1   7.999767
Bob 7   2   7.984759
Bob 7   3   7.365404
Bob 7   4   7.656814
Bob 8   1   7.882578
Bob 8   2   7.758508
Bob 8   3   4.55524
Bob 8   4   7.540994
Frank   1   1   9.481814
Frank   1   2   8.193099
Frank   1   3   8.398606
Frank   1   4   11.7037
Frank   2   1   9.949564
Frank   2   2   8.107129
Frank   2   3   9.163364
Frank   2   4   10.6489
Frank   3   1   9.327477
Frank   3   2   8.012667
Frank   3   3   8.249733
Frank   3   4   8.265833
Frank   4   1   9.037129
Frank   4   2   8.011473
Frank   4   3   9.851276
Frank   4   4   9.407426
Frank   5   1   9.109919
Frank   5   2   8.015916
Frank   5   3   9.295068
Frank   5   4   8.891632
Frank   6   1   8.259335
Frank   6   2   8.0005
Frank   6   3   8.595918
Frank   6   4   8.371596
Frank   7   1   7.938315
Frank   7   2   7.985911
Frank   7   3   7.619531
Frank   7   4   7.396689
Frank   8   1   7.448111
Frank   8   2   7.781902
Frank   8   3   5.067086
Frank   8   4   5.147675
Janet   1   1   8.421558
Janet   1   2   8.049732
Janet   1   3   8.737006
Janet   1   4   9.225913
Janet   2   1   9.93779
Janet   2   2   8.790311
Janet   2   3   10.30329
Janet   2   4   12.84334
Janet   3   1   9.853942
Janet   3   2   8.112191
Janet   3   3   8.553654
Janet   3   4   14.68811
Janet   4   1   8.088195
Janet   4   2   8.035893
Janet   4   3   8.689999
Janet   4   4   8.565889
Janet   5   1   8.90175
Janet   5   2   8.082496
Janet   5   3   12.3517
Janet   5   4   9.292084
Janet   6   1   8.042006
Janet   6   2   8.031552
Janet   6   3   8.23479
Janet   6   4   8.092882
Janet   7   1   5.905284
Janet   7   2   7.99629
Janet   7   3   7.978668
Janet   7   4   7.983601
Janet   8   1   7.768969
Janet   8   2   7.910555
Janet   8   3   5.9105
Janet   8   4   6.014394
Bob 1   1   8.680909
Bob 1   2   8.090483
Bob 1   3   8.846608
Bob 1   4   8.216097
Bob 2   1   9.23454
Bob 2   2   8.072461
Bob 2   3   9.365295
Bob 2   4   8.66944
Bob 3   1   8.700653
Bob 3   2   8.021997
Bob 3   3   10.73211
Bob 3   4   8.270761
Bob 4   1   8.621898
Bob 4   2   8.221656
Bob 4   3   8.873718
Bob 4   4   10.14723
Bob 5   1   8.612726
Bob 5   2   8.013137
Bob 5   3   8.854139
Bob 5   4   10.05516
Bob 6   1   8.238818
Bob 6   2   8.002169
Bob 6   3   8.283516
Bob 6   4   8.060694
Bob 7   1   7.811573
Bob 7   2   7.972366
Bob 7   3   7.550927
Bob 7   4   7.347237
Bob 8   1   7.552504
Bob 8   2   7.821391
Bob 8   3   6.153354
Bob 8   4   5.286279
Frank   1   1   8.521943
Frank   1   2   8.054066
Frank   1   3   8.235211
Frank   1   4   8.187873
Frank   2   1   9.711441
Frank   2   2   8.05149
Frank   2   3   10.82414
Frank   2   4   10.43218
Frank   3   1   11.1396
Frank   3   2   8.341912
Frank   3   3   8.197568
Frank   3   4   10.77953
Frank   4   1   9.186246
Frank   4   2   8.231934
Frank   4   3   9.107861
Frank   4   4   9.336874
Frank   5   1   8.156753
Frank   5   2   8.033916
Frank   5   3   11.35433
Frank   5   4   9.261594
Frank   6   1   8.309988
Frank   6   2   8.03288
Frank   6   3   8.337066
Frank   6   4   8.167594
Frank   7   1   7.240201
Frank   7   2   7.947292
Frank   7   3   6.137034
Frank   7   4   7.598853
Frank   8   1   5.868138
Frank   8   2   7.896514
Frank   8   3   5.148703
Frank   8   4   6.364151

Erik Ruzek · Answer 1 · 2020-03-25T20:21:35.400

1

The short answer is that the two models are not equivalent as specified. Without knowing what software you are using, it is hard to give you more than that. Mixed model code and how you specify crossed effects differs from software to software. Here are a couple of examples of common software packages we see on CV. If you are using R, then the code you would want to use would be something like

library(lme4)
lmer(outcome ~ instrument + (1|operator) + (1|operator:instrument), data=df)

If you were using Stata, then you would want to use:

mixed outcome i.instrument || operator: || instrument:, reml

These are two common software programs used for mixed modeling, but of course there are others.

Edit: Regarding the standard errors, you need to dig into the maximum likelihood estimation machinery. In words, "the curvature of the likelihood function at the ML estimate is used to inform the variability of the sampling distribution (McNeish, 2017)." A sharp curvature would lead to smaller standard errors (more certainty) while a gradual curvature would lead to larger standard errors (less certainty). The degrees of freedom issue is not something I can speak to because I have never seen such output from a mixed modeling routine as it relates to individual regression parameters. You should consult with the software developers of the program you are using to understand how they are calculating those.

The McNeish (2017) article I quoted is highly informative on REML and ML estimation of mixed models. In that article, Dan suggests reading Chapter 3 of Craig Enders' 2010 book on missing data. I don't remember that chapter in particular, but I can attest to that being a great resource on MI.

edited Mar 25 '20 at 20:21

answered Mar 23 '20 at 20:29

Erik Ruzek

3,297
10
18

I have repeated the analysis in R. The two models are: * lmer(new.Y ~ Instrument + (1 | Operator) + (1 | Operator:Instrument), data = df); * lmer(new.Y ~ Instrument + (1 | Operator:Instrument), data = df) and the results are exactly the same as above. So my question still holds, independently of the software. – user7064 Mar 24 '20 at 06:53
1

I will update my answer a little later today @user7064. Those two model specifications are very different in `lmer`. The random effects with `(1|Operator:Instrument)` are essentially asking for a separate intercept for all combinations of the two factors. That model only gives you a single variance component, other than the residual. It's shoving all the variance into that single term, and doesn't tell you how much variance is due to instrument vs. operator. The other specification parses out the operator from the instrument variance. – Erik Ruzek Mar 24 '20 at 13:26
thank you. I do understand this difference. However, as you can see in the output, it does not make a difference for the fixed effects... except for the SEs and DFs, and my question is why these differences. Thank you – user7064 Mar 24 '20 at 13:29
How many combinations of operator and instrument do you have? – Erik Ruzek Mar 24 '20 at 21:43
3 operators and 4 instruments (crossed factors) – user7064 Mar 25 '20 at 06:06
@user7064, updated my answer to address the standard error issue. I don't know how your software is calculating those DFden estimates. I'm not sure what that even is. – Erik Ruzek Mar 25 '20 at 20:22

Sextus Empiricus · Accepted Answer · 2020-03-25T23:02:46.367

Let's look at a simpler example: the mean performance of school kids in a particular area is estimated by sampling 100 kids in the area. Then normally you compute the mean and base the error of the estimate of the mean on the residuals and incorporate a factor that scales with the square root of the sample size $1/\sqrt{n}$ (the standard error). But say now you sampled those kids only from 4 schools and the schools themselves have variation in performance... Is it correct to use 100 instead of 4 as the sample size to compute the standard error?

No, so you consider the schools as a random effect and incorporate it in the number of measurements to determine the standard error. This will now be larger (because your sample size is effectively smaller).

So this is what makes a difference. In the second situation you consider more structure which reduces your effective sample size and increases the error estimate.

It looks like operator * instrument is not computed in the first case. Then you are comparing a model where in one case the random effect is only operator level and the other case operator*instruments.

See the difference in degrees of freedom 8 versus 186. So what happens is that the sample size of about two hundred data points for each instrument is reduced to effectively 8 degrees of freedom because those points are clustered in only 3 operators. (You do not get a degree of freedom 3-1, because the calculations of degrees of freedom are not so harsh but are making some weighted considerations of the group/sample sizes. See also: How to determine Degrees of Freedom in Linear (Mixed Effect) Regression)

Thank you. I wanted to award the bounty... but it seems I cannot. I guess it will be added automatically later on... — user7064, Mar 26 '20 at 10:24
@user7064 If you give an more complete description of your model I could provide a more full explanation with some intuitive graphics. I am wondering about the effects of the instruments, are they some sort of slopes (which require some other variable) or are they deviations from the intercept? — Sextus Empiricus, Mar 26 '20 at 10:51

score 0 · Answer 3 · answered Mar 25 '20 at 17:36

The basic answer to why are the standard errors errors of the fixed effects are different is basically due to the different structure in the random effects. Now the question you should be asking as well is: should you be looking at the standard error estimates of the fixed effects in the first place?

If you are looking to perform inference (e.g. Wald tests) on the fixed effect parameters, then no. See, restricted maximum likelihood estimation works by estimating the fixed effects by other technique (usually OLS or GLS) and then fitting the random effects on the residuals of the first procedure. This means that any statistic one analysis based on REML can only describe the random portion of the model, not the fixed portion.

This means that the standard errors are the same in both models minus what is estimated by random effects (this part I may be wrong on what the math exactly translates to).

The reason why full maximum likelihood estimation is not default is that it underestimates variance components for low sample size due to not taking into account the estimated fixed parameters. In that sense REML works similar to Bessel Correction for variance estimation.

Sources:

section 4.3.2 of Applied Longitudinal Data Analysis by Singer and Willett

difference in standard errors between 2 seemingly equivalent models

3 Answers3