0

For my undergrad thesis I wanted to build a multidimensional index of financial inclusion that would include variables of access and use of financial services in the states of Mexico. I have a set of 16 variables for 32 observations. Since financial inclusion itself can't be quantified, I was told PCA would be the right way to build an index with these related variables.

I want to achieve something similar to this: https://www.bis.org/ifc/publ/ifcb47p.pdf

What I can't seem to understand is how I am supposed to "normalize the weights to sum 1" so I can tell what's the percentage of the total index determined by each variable.

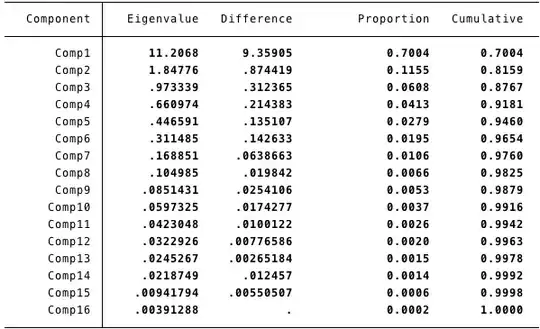
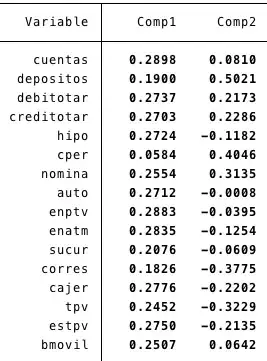
I get the following results when doing the PCA: Results from PCA in Stata PC1 and PC2

I would extremely appreciate if someone could help me out figure this or point me to a book or paper that can elaborate on the subject, and also advise me if PCA is the correct methodology for I want to achieve or if my attempts are nonsensical.

Thanks!

Felipe Lastra
  • 1
  • From [here](https://stats.stackexchange.com/a/143949/3277): `Rescaled loading squared has the meaning of the contribution of a pr. component into a variable`. `Eigenvector value squared has the meaning of the contribution of a variable into a pr. component`. These are the two general guidelines. Now, your second table are the "loadings". Since the sum of eigenvalues (1st table) = 16, the number of items, I conclude that your analysis was "correlation-based" PCA, then loading = rescaled loading. Eigenvectors - they are not present in your output. – ttnphns Mar 23 '20 at 08:15
  • This Q https://stats.stackexchange.com/q/133492/3277 _might_ be relevant perhaps and would be looked. – ttnphns Mar 23 '20 at 08:21

0 Answers0