0

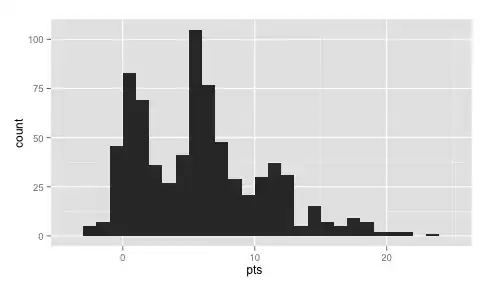
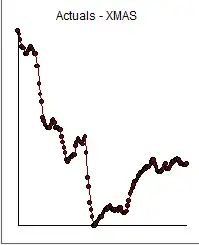
I am running a mlr in python on a dataset with 2D feature vectors, X1 and X2 on a single response, Y. The data ends up being funnel-shaped, as below: X1 v Y, with the colors being X2. Original Data, X1 v Y with the colors marking X2

It was difficult to fit any linear fit here, so I tried to do a log-log transform with the following results.

Log-Log Transformation

As you can see above the funnel is narrowed. Without going into too much detail, my r-squared score improved to about 0.79, but my mean absolute error was still high. As I am trying to use this model for predictions, I am trying to reduce the mean error as much as possible. I also tried a log transformation of the response only, and tried a polynomial fit.

Polynomial Fit

However the results ended up being not much better than the log-log transform. MAE went down to about 0.35 (which I interpret as about a 35% deviation from the mean?) and. r-squared at about 0.79.

Is there anything else I can do to transform the data so a linear or mlr or polynomial fit can work? I need as low error as possible. Thank you!!!!

EDIT:

The data is a data set of solar irradiance and cloud cover. Irradiance is measured as Global Horizontal Irradiance "GHI" and cloud cover as a decimal between 0 and 1 inclusive. The target variable is a type of solar irradiance called Diffuse Horizontal Irradiance "DHI" which results from reflected or scattered sunlight falling upon a measurement device.

In all data here, GHI (the total measured sunlight) is on the X axis, and the diffused (reflected) irradiance on the Y axis. Cloud cover is indicated by the colors. Hope this helps.

Tuomas Talvitie
  • 29
  • 5
  • 1
    You are coy about what the data really are. I agree that heteroscedasticity is evident but the reasons may include constraints on the variables, either singly or jointly. The edges to the scatter are sharper than is common. The first plot is X1 versus Y which I take to mean that Y is on the horizontal axis, although usages differ (see https://stats.stackexchange.com/questions/146533/versus-vs-how-to-properly-use-this-word-in-data-analysis). The colour coding of X2 does nothing for me, and I suggest that you plot a scatter plot matrix with Y, X1, X2 and tell us their ranges [minimum, maximum]. – Nick Cox Mar 21 '20 at 11:57
  • 1
    The log transform overcorrects, which sometimes occurs if variables are bounded. If in principle they are limited, that is important information. – Nick Cox Mar 21 '20 at 11:59
  • MAE when the response is logged is in quite different units from the original. It can even go up if you forget about the units. – Nick Cox Mar 21 '20 at 12:02
  • What is the colo[u]r coding in any case? It looks like a rainbow scheme which makes sense in physics but not in psychology (what the mind thinks) or physiology (what the eye sees). – Nick Cox Mar 21 '20 at 12:30
  • Sorry if I was being coy, I was just trying to simplify things. X1 is a measurement of Solar Irradiation picked up by a sensor. X2 is a measure of cloud cover from 0-1. Y is a measure of solar radiation picked up by indirect irradiation (like bouncing off clouds, other surfaces, etc) – Tuomas Talvitie Mar 21 '20 at 13:20
  • So given this type of data, is a log transformation advisable ? – Tuomas Talvitie Mar 21 '20 at 13:29
  • Logit of cloud cover could be a better idea. – Nick Cox Mar 21 '20 at 17:43
  • Some sample data might elicit better replies (than mine). A random sample of say 100 observations might be enough. – Nick Cox Mar 22 '20 at 12:11
  • I mean that cloud cover is continuous from 0-1. So 0.1,0.2,0.3....1. Should it still be a logit transformed? – Tuomas Talvitie Mar 23 '20 at 19:04
  • That is my suggestion, so long as you don't have exact zeros or ones. – Nick Cox Mar 23 '20 at 19:05
  • The graphs give some flavour of your problem, but I don't think a serious answer is possible without more information. – Nick Cox Mar 23 '20 at 19:06
  • Oh, unfortunately the values are inclusive. Why do you propose a logit transform? What information would you like me to provide? I'm sorry I am not too well versed in regression analysis so I apologize if I make errors. – Tuomas Talvitie Mar 23 '20 at 19:07
  • Catch-22 here: without real or realistic data to experiment on, which I suggested a few comments back, I can only guess. And I've already commented that I can't decode your colour coding for X2, which you still haven't explained. Rather, it's a good general principle that logit of proportions often works well. I am voting to close. – Nick Cox Mar 23 '20 at 19:17
  • Please add this additional info (together with more, as asked for) as an edit to the post! Not everybody read comments, especially not when they are many as here. Then, after adding info as edit, clean up the comments by deleting ... – kjetil b halvorsen Mar 24 '20 at 18:25
  • My last guess: model the ratio DHI/GHI as a function of cloud cover. – Nick Cox Mar 25 '20 at 08:25

1 Answers1

0

A whole slew of transformations didn't work, now resorting to fitting a GLS model.

Tuomas Talvitie
  • 29
  • 5