Goodness of Fit and transformations

Question

I have a $10,000$ observations (say vector $x$) which I think follows some distribution function $F$. Now, to check this I want to apply Goodness of Fit test. My question is, Is applying goodness of fit directly on this set of observation (test for $F$) same as applying goodness of fit on $y$ checking for $Unif(0,1)$ where $y_i=F(x_i)$?
If not, Under what conditions will it fail?
I know $F(x)$ follows uniform and $F^{-1}(y)$ follows $F$(if the Hypothesis is true that is)
But if the Hypothesis is false, is it possible that the second test passes where the first failed?

Answer 1

Suppose I have 10,000 observations precisely from $\mathsf{Gamma}(shape=5, rate=0.1).$ Generate them in R as follows:

set.seed(2020);  x = rgamma(10^4, 5, .1)

(1) Then, because we know the distribution and its parameters, a basic Kolmogorov-Smirnov test in R, finds that my observations are consistent with $\mathsf{Gamma}(shape=5, rate=0.1).$

ks.test(x, pgamma, 5, .1)

        One-sample Kolmogorov-Smirnov test

data:  x
D = 0.0096536, p-value = 0.309      # Not rejected at 5%
alternative hypothesis: two-sided

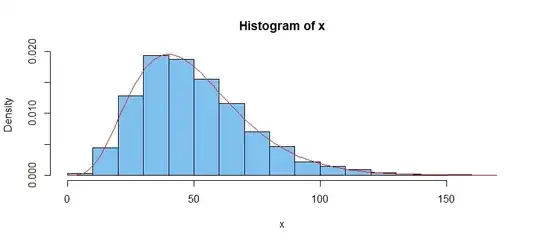
Here is a histogram of the large sample, along with the density function of $\mathsf{Gamma}(shape=5, rate=0.1).$

hist(x, prob=T, col="skyblue2")
curve(dgamma(x, 5, .1), add=T, col="red")  # dummy argument 'x' req'd

(2) You might take the apparent good fit of the histogram to the intended density function as an informal (non-quantitative) visual goodness-of-fit test.

(3) You are correct that transforming by the CDF gives a standard uniform distribution. (In fact, the K-S test uses this transformation as its first step, essentially looking at the largest deviation of the empirical CDF of the transformed data from the exact CDF of standard uniform, and using a distribution based on the Brownian Bridge.)

hist(pgamma(x, 5, .1), prob=T, col="skyblue2")
curve(dunif(x, 0, 1), add=T, col="red", n=5000)  # 'n=5000' for good plot

Then you could count the number of observations in each of the 20 histogram bars $(Y_1, \dots, Y_{20})$ and do a straightforward chi-squared test using the statistic $$Q = \sum_{i=1}^{20} (Y_i - E_i)^2/E_i,$$ where all $E_i = 10,000/20 = 500.$ Under the null hypothesis that data follow the intended gamma distribution, $Q \sim \mathsf{Chisq}(df=19).$

In R, you could fetch the 20 counts $Y_i$ as follows:

hist(pgamma(x, 5, .1), plot=F)$counts
 [1] 459 471 488 534 493 544 511 521 502 528
[11] 448 495 473 521 525 522 462 486 513 504

Then the chi-squared GOF test 'almost' rejects at the 5% level:

 q = sum((y-500)^2/500);  1-pchisq(q, 19)
 [1] 0.08381428

Note: A problem with any goodness-of-fit test on such a large sample is that even the slightest departure from the intended distribution (even one that is not of practical importance), can lead to rejection. Partly for this reason, some goodness-of-fit tests in statistical software are programmed not to accept samples larger than about 5000.