0

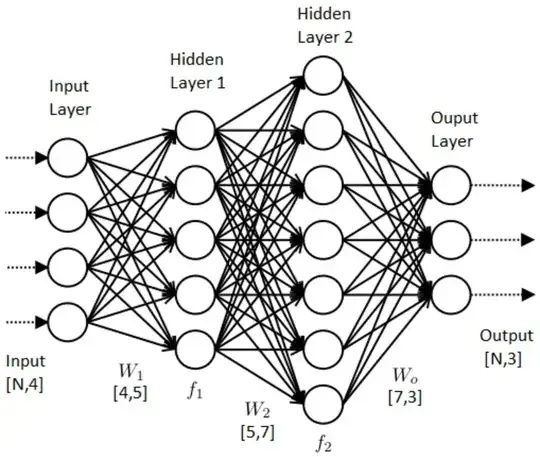
enter image description here

Often you see diagrams like these.

Which makes me wonder what is the definition of a layer, because as it is drawn, it is very vague.

For example, when people say a fully connected layer, what do they mean by a layer?

From the diagram, it seems that:

  1. The input layer is a set of components associated with your input vector, as well as the value of the weights going to the hidden layer, i.e., let your input vector $x = (x_1, \ldots, x_n)$, then the input layer is the set $$L_i = \{x_1, \ldots, x_n\} \cup \{w_{ij}\},$$ where $w_{ij}$ are the weights associated with the input layer.

  2. The hidden layer as well as the output layer consists of a set of activation functions $a_i$ which transforms the input $x$ into a set of outputs $o_i$, along with the weights going into the next hidden layer,i.e., $$L_H = \{a_i\} \cup \{o_i\} \cup \{w_{ij}\} $$.

Is my interpretation correct?

Olórin
  • 674
  • 5
  • 16

1 Answers1

0

The so-called "Input Layer" is not a layer actually. Rather it is an input vector. The layering starts when each node in a layer has summation of the weighted inputs (from input vector or previous layer) and an activation function. Thus the first hidden layer is the first layer accordingly.

model = Sequential()
model.add(Dense(50, input_shape=(10), activation='relu'))
model.add(Dense(1, activation='sigmoid'))

The second line in the above code in Python adds a hidden layer as a first layer with the input vector as one of the parameters.

PS Nayak
  • 160
  • 1
  • 7