Making a discrete probability question continuous

Question

I'm trying to figure out how many coin flips you'd need to have a greater than 50% chance of having seen a heads, given a biased coin with heads probability $p$.

From this question we can see that the probability of it taking $k$ flips is as follows

$$P(X = k) = p(1-p)^{k-1}$$

So if we want to find the probability of it taking $k$ flips or fewer, we can just sum up all the probabilities from 1 to k

$$P(X \leq k) = \sum_{n=1}^k p(1-p)^{n-1}$$

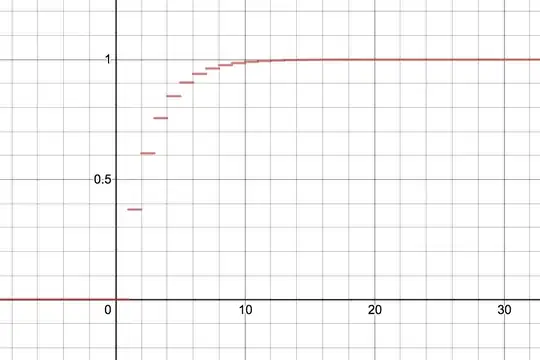
Using Desmos we can see that what we get looks exactly like we'd expect, with an asymptote to 1 that becomes too small to see past around 15

But I want to figure out how many flips you'd need to pass 50% probability, and that means allowing for fractional flips, so let's switch our summation to integration

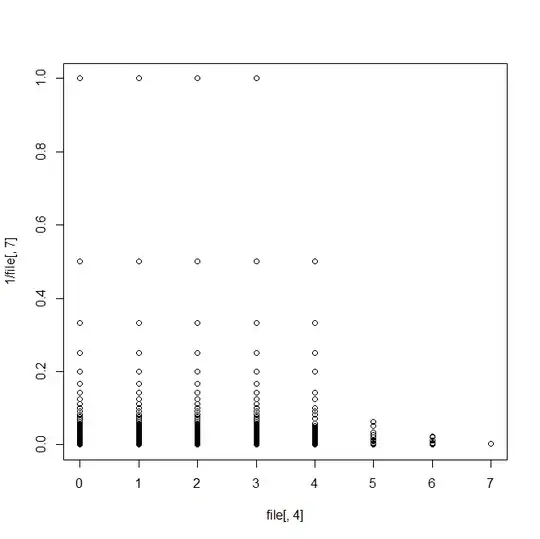
$$P(X \leq k) = \int_{1}^k p(1-p)^{n-1} \ dn$$

But now, this happens! The asymptote now only goes to 0.8, and at 1 flip the probability is listed as zero! Why?

Answer 1

This shouldn't surprise you because integral and summation asymptotes can naturally differ. For example, take the following:

$$\int_1^\infty \frac{1}{x^2}dx=-\frac{1}{x}\bigg\vert_1^\infty=1$$ but (see Basel Problem): $$\sum_{x=1}^\infty \frac{1}{x^2}=\frac{\pi^2}{6}$$

Continuous analogue for the geometric distribution is actually the exponential distribution.