A good example of this is provided by Glen_b -Reinstate Monica at https://stats.stackexchange.com/a/189633/40036 . The question there was slightly different -- asking if normally distributed $X$ and $Y$ must be jointly normal for $X+Y$ to be normal -- but the construction there also answers your question here (because the constructed $X$ and $Y$ happen to be uncorrelated). I'll expand on that answer a bit to establish that it meets your requirements.
The construction first draws $U,V\overset{iid}{\sim}\mathcal{N}(0,1)$, and then constructs $X$ and $Y$ as follows:
$$
X = \left\{\begin{array}{cc} \max(U,V) & \text{if}~U,V\geq 0 \\ -\min(-U,V) & \text{if}~U<0,V\geq 0 \\ \min(U,V) & \text{if}~U,V<0 \\ \min(U,-V) & \text{if}~U\geq 0,V<0\end{array}\right. \\
Y = \left\{\begin{array}{cc} \min(U,V) & \text{if}~U,V\geq 0 \\ \max(-U,V) & \text{if}~U<0,V\geq 0 \\ \max(U,V) & \text{if}~U,V<0 \\ -\max(U,-V) & \text{if}~U\geq 0,V<0\end{array}\right.
$$
Lifting a very nice figure from the linked answer, this construction basically limits $(X, Y)$ to only half of the x-y plane -- the areas in purple are where $(X, Y)$ occur with twice the density of the standard bivariate normal distribution and the areas in white are where $(X, Y)$ do not occur.
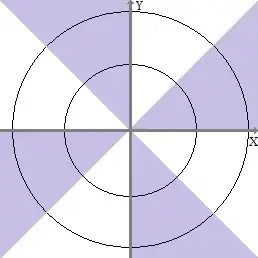
We can now establish each of your desired properties for the distribution (we will denote its pdf $f_{XY}$):
$X$ and $Y$ are not independent: This is visually apparent. For instance, if $X=1$ then $Y$ can only take values in $(-\infty, -1]\cup[0,1]$.
$X$ and $Y$ are non-degenerate normal random variables: $f_X(x) = \int_{0}^\infty f_{XY}(x,y)+f_{XY}(x,-y) dy$. From the plot it is apparent that one of $f_{XY}(x,y)$ and $f_{XY}(x,-y)$ will take twice the value of the standard bivariate normal pdf evaluated at that point, while the other will take value 0. Since the standard bivariate normal is symmetric around the line $y=0$, we conclude that $f_X(x)=\phi(x)$, and therefore $X\sim\mathcal{N}(0,1)$. A symmetric argument yields $Y\sim\mathcal{N}(0,1)$.
$X$ and $Y$ are uncorrelated: Consider arbitrary $x\geq 0, y\geq 0$. From the plot we read that $f_{XY}(x,y) = f_{XY}(-y,x)$, and we use the symmetry to conclude that $E[XY|Y\geq 0] = 0$. A similar argument yields $E[XY|Y\leq 0] = 0$, so we conclude that $X$ and $Y$ are uncorrelated.
$X+Y$ is a non-degenerate normal random variable: $f_{X+Y}(u) = \int_0^\infty f_{XY}(\frac{u}{2}-z,\frac{u}{2}+z)+f_{XY}(\frac{u}{2}+z,\frac{u}{2}-z)dz$. From the plot, it is apparent that exactly one of $f_{XY}(\frac{u}{2}-z,\frac{u}{2}+z)$ and $f_{XY}(\frac{u}{2}+z,\frac{u}{2}-z)$ will take twice the value of the standard bivariate normal pdf evaluated at that point, while the other will take value 0. Since the standard bivariate normal pdf is symmetric around the line $x=y$, we conclude that $f_{X+Y}$ equals the pdf of the sum of the components of a standard bivariate normal distribution, meaning $X+Y\sim\mathcal{N}(0,2)$.
