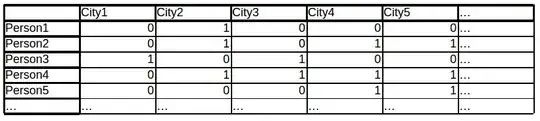
Here someone recommended box-plots for visualization.
But the following graph made me realize how box-plots can fail to meaningfully depict the Wilcoxon signed-rank test or sign tests in general: In some cases you can't even guess the "direction" of significant results.
It's even worse: In non-normal data, there exist theoretical cases with all 5 of [median, 2 quartiles and 2 extreme points] of sample_1 being the 2-fold of sample_2, in which even the most skeptical statisticians might think to know the direction of the sign-test. But even in such an extreme case, it's possible that the "direction" of a significant result is opposite of what the box-plot would suggest.
So my question is: Do you also see this problem and if yes; what to do?
Should I just mark the group with the higher (+)sign total? I know I could plot the ranks instead, but I want to show information of the parametric values. Maybe I am wrong by design and I should not ever pick a sign-test if I want to show parametric values on the y-axis and I should instead use the paired t-test? Or maybe I should just plot all my individual values and only go for box-plots given high N?