The SSE of the LASSO solution $\tilde\beta$ in comparison to the SSE of the OLS solution $\hat{\beta}$ can be expressed as
$$(X (\tilde\beta-\hat{\beta})) \cdot (X (\tilde\beta-\hat{\beta})) = (\tilde\beta-\hat{\beta}) X^TX (\tilde\beta-\hat{\beta}) $$
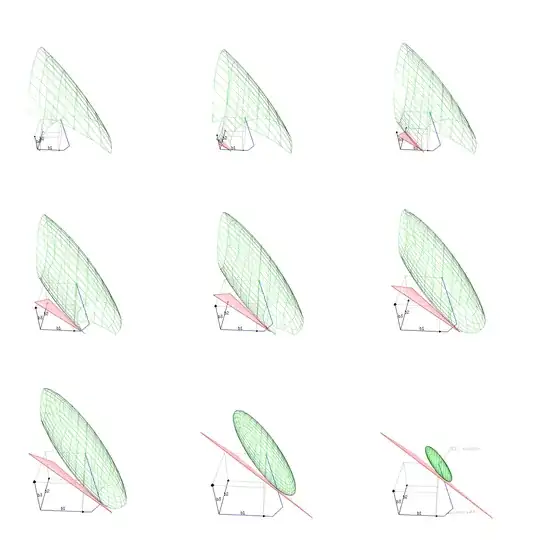
You can see this graphically as some ellipsoid surface (as the image below which I copied from this question).
Limit behaviour of $ \frac{1}{n}\sum_{i}^{n}||y_{i} - \textbf{x}_{i}\tilde\beta||_{2}^{2} $
This ellipsoid will depend on the particular sample (based on which $\hat\beta$ and $X^TX$ will vary) but for $n \to \infty$ you will get that the variation in this surface becomes smaller.
Limit behaviour of $ \frac{\lambda_{n}}{n}\sum_{j=1}^{p}|\tilde\beta_{j}|$
If $\{\lambda_{n}\}$ is $o(n)$ then $\lbrace\frac{\lambda_{n}}{n}\rbrace$ is $o(1)$ and approaches zero.
So the first term in the cost function will approach some quadratic function of $\tilde\beta$ and the second term will approach zero. The lasso solution that minimises the sum of these terms will approach the true $\beta$ (The reasoning here is very intuitive but I am sure there is some reference for that).
The consequence is that $\{t_n\} - \sum_{j=1}^{p}|\beta_{j}| $ will approach zero (where $\beta_j$ refers to the true coefficients).