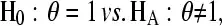0

I am reading a tutorial on the Dirichlet distribution: http://mayagupta.org/publications/FrigyikKapilaGuptaIntroToDirichlet.pdf

and I think there is a typo in Step 2 of the stick-breaking model of the Dirichlet distribution:

enter image description here

Specifically, I think some of the $u_i$ should be $q_i$. If pieces with lengths $u_1,u_2,...,u_{j-1}$ have been broken off, how can the length of the remaining stick be $\prod_{i=1}^{j-1}(1-u_i)$, shouldn't it be $1-\sum_{i=1}^{j-1}u_i$? It would make sense if the it the length of the remaining stick were $\prod_{i=1}^{j-1}(1-q_i)$. I believe the last line of Step 2 should also be $q_i$ instead of $u_i$. Please tell me if I am wrong, I find this quite confusing.

Noppawee Apichonpongpan
  • 469
  • 3
  • 11
  • 1
    It looks right to me: at each step, a proportion $1-u_j$ of whatever is remaining will be left for the next step. The calculation at the end of step 2 is done in an obscure way; it's only saying that when you multiply the first $j-1$ of these fractions by the last one, you get the product of all $j$ fractions. – whuber Feb 25 '20 at 18:34
  • Ah, right, I get it now. "For $2 \le j \le k-1$, if $j-1$ pieces, with $\mathbf{lengths}$ $ u_1,u_2,...,u_{j-1}$, have been broken off, the length of the remaining stick is $\prod_{i=1}^{j-1} (1-u_i)$" <<< This really tripped me up. – Noppawee Apichonpongpan Feb 25 '20 at 18:46
  • It's a strange description. I would have reversed the Beta parameters and replaced each $u_i$ by $1-u_i,$ because it simplifies the description and the formulas. – whuber Feb 25 '20 at 18:49
  • 1
    Incidentally, if you're curious, the derivation on pp 13-14 (of the Dirichlet from Gamma distributions) is discussed on CV at https://stats.stackexchange.com/questions/36093. I think you might find our approach a little less cumbersome. – whuber Feb 25 '20 at 18:51
  • @whuber Thank you! – Noppawee Apichonpongpan Feb 26 '20 at 03:40

0 Answers0