Consider the following model
$$y_i = \sigma_{c(i)} + \mathbf x_i^\top\beta + u^y_i $$ $$\sigma_{c} = z_c\lambda + \eta_c$$
where for all $i$
$$\mathbb E[u^y_i \lvert x_i] = 0$$
Data is given for a random sample $\{y_i,\mathbf x_i,z_{c(i)}\}_{i=1}^N$ leaving $u^y_i, \sigma_c, \eta_c,\lambda$ and $\beta$ unobserved.
Intuitively the model can be interpreted as a two level model where $i$ is an observed worker getting wage $y_i$ in city $c$ and $z_c$ are covariates observed on a city level while $\eta_c$ are unobserved city specific factors affecting wage additively through $\sigma_c$. The function $c(i)$ simply connotes the city where individual $i$ works.
Clearly estimation of the first equation can be carried out using city specific dummies which would result in an estimate $\hat \sigma_c$ for each city (I have very many observations for each city/group so I guess this is ok). Then in order to estimate $\lambda$ the second stage regression
$$\hat \sigma_c = z_c \lambda + \eta_c$$
is performed. Can such an approach be justified (give consistent estimate of $\lambda$) when
$$\mathbb E[\eta_c \lvert z_c] = 0$$
but
$$\mathbb E[\eta_c \lvert \mathbf x_i] \not = 0,$$
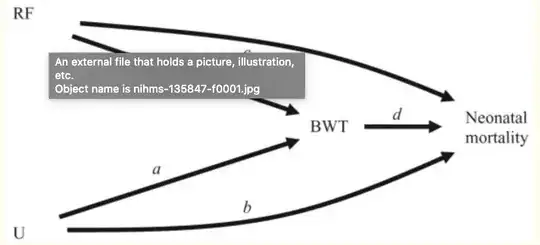
perhaps by considering the DAG of the model which I think could go something like this 
which should be implemented in the following code, which I believe shows that the approach works. But I am not sure how to show it using for example arguments from Pearl authorship on DAG's or any other argument given the assumptions.
library(data.table)
library(lfe)
N <- 100000
C <- 300
# Make index over what cities individual worker are in
city_index <- sample(1:C,N,replace=TRUE)
# Make unobserved city productivity effect eta and observed z
eta <- 6*runif(C)
z <- 2*runif(C)
# Calculate city level effect
a <- 1
c_i <- z[city_index]*a + eta[city_index]
# Simulate worker specific skill x
u_x <- rnorm(N)
x <- u_x + c_i
b <- 2
u_y <- rnorm(N)
# Simulate wages
y <- c_i + x*b + u_y
mydata <- data.table(wage=y,city=city_index,skill=x,city_chr=z[city_index])
model_1 <- felm(wage ~ skill + city_chr,data=mydata)
model_2 <- felm(wage ~ skill - 1|city,data=mydata)
model_1
model_2
city_data <- data.table(getfe(model_2))[,.(idx,effect)]
city_data$city_chr <- z
lm(effect ~ city_chr,data=city_data)
plot(city_data$effect[city_index],c_i)