Is it okay to take the mean of p-values

Question

I have two samples, that I cannot assume come from the same distribution, with different means and variances and different sample sizes. The sizes are very different so I iteratively subsample the biggest one and perform a welsch test between with subsample and the other.

Let's say that in those iterations 8 out of 10 times I can reject H0.

Does it make sense to take the mean p-value out of those iterations as an indicator of significance?

update

Some problem details needed. The variable I am interested in comparing between the two groups is a mean frequency. The user takes can take some actions multiple times a month. This frequency is practically the actions per day for the month over the number of days in the month.

I hypothesize that the users in one group (the larger group) have a higher frequency than the users on the alternative group (which is smaller). The reason why I am performing a T-test is to validate this assumption.

Answer 1

If your group sizes are large enough, you are well powered to detect effects so small as to essentially be useless. Here is an example in R. I generate 200,000 observations from two groups whose means differ by 0.01.

library(tidyverse)


replicate(1000,{
  x = rnorm(200000)
  y = rnorm(200000, 0.01, 1)

  t.test(x,y)$p.value<0.05
}) %>% mean

I correctly reject the null 88% of the time, but the result of my test is quite uninteresting because the difference is so small (EDIT: I guess small is relative here. I'm sure a 1% difference in some applications is worth thousands of dollars). As I said in the comments, no two groups are exactly identical and so with enough data, that will be demonstrated.

So what are some ways we can deal with this? We can abandon significance testing all together and instead opt for estimation. Whatever your metric of interest is, you could instead create confidence intervals for the mean outcome per group. I highly suspect this is for an internet AB test, so you could say something along the lines of "our intervention yielded an effect between x and y, as compared to control which was w and z". You could use the t-test to compute a confidence interval for the difference in the means, which might be even more useful.

Answer 2

It seems that the OP is mainly concerned with conducting a t-test for unequal sample sizes.

However, imbalanced sample sizes are in general not a huge problem when applying the t-Test. The t-test is actually very stable against sample size characteristics as deviations from normal distribution and imbalanced sample sizes (if sample sizes are large enough!). Small simulations are following to illustrate this:

p.value <- c()
n.sim <- 1e5
for(i in 1:n.sim){
  x1 <- rnorm(n=100,mean=1,sd=1)
  x2 <- rnorm(n=1000,mean=1,sd=1)
  p.value[i] <- t.test(x1, x2)$p.value
}
sum(p.value<0.05)/n.sim
> [1] 0.05083

As you see, no increase of type I error rate. I have assumed that both samples come from a normal distributions, though. Let's consider a completely different distribution, e.g. two very different Gamma distributions but with the same mean (mean is shape divided by rate):

p.value <- c()
n.sim <- 1e5
for(i in 1:n.sim){
  x1 <- rgamma(n=100,shape=1,rate=1)
  x2 <- rgamma(n=1000,shape=10,rate=10)
  p.value[i] <- t.test(x1, x2)$p.value
}
sum(p.value<0.05)/n.sim
> [1] 0.05749

Slightly increased type I error rate. Whether this is serious enough to prevent from using a t-test is debatable. Taking a look at the distribution of p-values might be insightful, too. Under the null hypothesis, p-values should be uniformly distributed, and it looks pretty much like it:

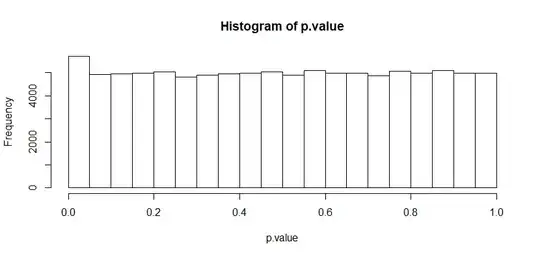
Note that this problem will become more serious, when your sample sizes are smaller than what I assumed, e.g. for the last example with the sample sizes being 10 and 100 instead, the type I error rate becomes 0.10177.

What happens if we take subsamples from the larger group, calculate the p.value each time, and then average these p.values?

p.value <- c()
pvalue2 <- c()
n.sim <- 1e5
for(i in 1:n.sim){
  x1 <- rgamma(n=100,shape=1,rate=1)
  x2 <- rgamma(n=1000,shape=10,rate=10)
  for(j in 1:10){
    x2.sub <- x2[((j-1)*100+1):(j*100)]
    pvalue2[j] <- t.test(x1, x2.sub)$p.value
  }
  p.value[i] <- mean(pvalue2)
}
sum(p.value<0.05)/n.sim
> [1] 0.03909

Seems something might be off with the type I error rate. But it gets really interesting if we take a look at the distribution of p-values. 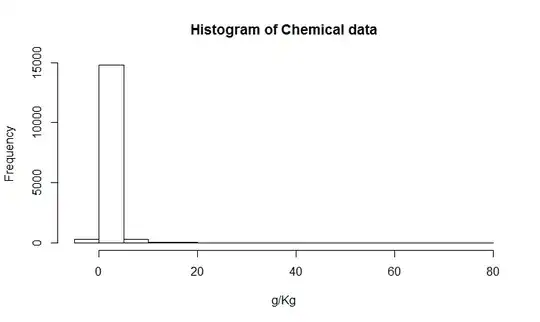Doesn't look like a uniform distribution at all anymore! With imbalanced sample sizes we are far better off than with taking the mean of p-values for several subsamples.