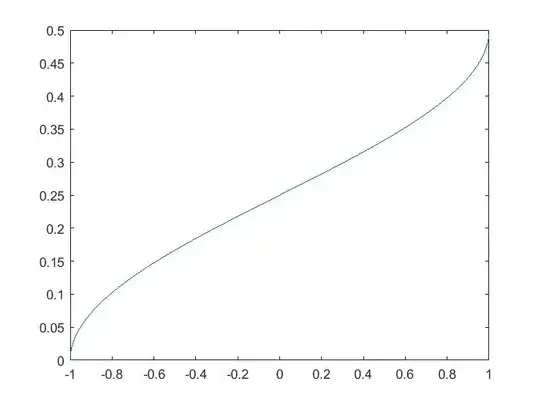
$\begin{bmatrix}\epsilon_{1}\\ \epsilon_{2}\end{bmatrix}\sim N(\begin{bmatrix}0\\0\end{bmatrix},\begin{bmatrix}1,\rho\\ \rho, 1\end{bmatrix})$. Show that the joint cdf evaluated at (0,0), i.e., $F_{\epsilon_{1},\epsilon_{2}}(0,0,\rho)\equiv Pr(\epsilon_{1}\leq 0, \epsilon_{2} \leq0)$ is monotonically increasing in $\rho \in (-1,1)$. Numerical calculation below (using 2000 grid points) shows that this is almost indeed the case. Thanks!
- 1,608
- 5
- 11
-
The analysis at https://stats.stackexchange.com/a/71303/919 should make this result obvious, because as $\rho$ increases, the probability assigned to the first quadrant corrresponds to an ever larger region for the standard bivariate Normal distribution under the *area preserving* "lifting" transformation $(x,y)\to (x, y+\rho x ).$ – whuber Feb 10 '20 at 03:37
-
Thank you very much. This link is indeed very helpful! – T34driver Feb 10 '20 at 05:11
2 Answers
Take independent standard normal random variables $X$ and $Y$. Then the joint distribution of $X$ and $\rho X-\sqrt{1-\rho^2}\,Y$ is the same as joint distribution of $\epsilon_1$, $\epsilon_2$. This is Cholesky's decomposition. Then
$$
\mathbb P(\epsilon_1\leq 0, \epsilon_2\leq 0) = \mathbb P\left(X\leq 0, \rho X-\sqrt{1-\rho^2}\,Y \leq 0\right)=\mathbb P\left(X\leq 0, Y\geq \frac{\rho}{\sqrt{1-\rho^2}}X \right)
$$
The function $\frac{\rho}{\sqrt{1-\rho^2}}$ is monotonly increasing in $\rho\in[-1,1]$. Therefore, if $\rho_1<\rho_2$ then $\frac{\rho_1}{\sqrt{1-\rho_1^2}}<\frac{\rho_2}{\sqrt{1-\rho_2^2}}$. Then for $X< 0$,
$$
\frac{\rho_1}{\sqrt{1-\rho_1^2}}X > \frac{\rho_2}{\sqrt{1-\rho_2^2}}X
$$
and if $Y$ is greater the first, it is definitely greater the second. So we have the inclusion of the events:
$$
\left\{X\leq 0, Y\geq \frac{\rho_1}{\sqrt{1-\rho_1^2}}X \right\} \subset \left\{X\leq 0, Y\geq \frac{\rho_2}{\sqrt{1-\rho_2^2}}X \right\}.
$$
This events are equal only when $X=0$ which has zero probability.
Therefore the probability of the first event is strictly less than the probability of the second, which means that $\mathbb P(\epsilon_1\leq 0, \epsilon_2\leq 0) $ is strictly increasing in $\rho$.
- 536
- 3
- 7
-
Thanks a lot! Your answer is quite elegant, and completely solved my problem. Seems the (0,0) here plays a crucial role, and when evaluated at other points this monotonicity in $\rho$ is not necessarily true. – T34driver Feb 10 '20 at 05:06
According to Formula 26.3.19 of Abramowitz and Stegun's Handbook of Mathematical Functions,
$$\int_0^\infty\int_0^\infty f(x,y;\rho)\;\mathrm dx\;\mathrm dy = \frac 14 + \frac{\arcsin \rho}{2\pi}$$ where $f(x,y;\rho)$ is the bivariate normal density of two standard normal random variables with correlation coefficient $\rho$. By symmetry, $\frac 14 + \frac{\arcsin \rho}{2\pi}$ is also the value of the joint CDF at the origin. Since $\arcsin\rho$ increases monotonically from $-\frac{\pi}{2}$ to $+\frac{\pi}{2}$ as $\rho$ increases from $-1$ to $+1$, this proves the desired result.
- 41,202
- 4
- 94
- 200
-
Thank you so much! This analytical formula for the integral is awesome, showing exactly what's going on with $\rho$. – T34driver Feb 10 '20 at 05:27