0

Frankly, this is an old topic, but I am hoping this is a new perspective. Though it is been a while, I am pretty familiar with PCA and all the linear algebra/math beneath it. I was thinking about using PCA for some task today and was following the standard recipe to normalize features before performing PCA, but couldnt wrap my mind around one detail.

Intuitively, if the dataset is multivariate Gaussian, the contour is an ellipsoid. What PCA does is removing the shorter orthogonal axis after a linear transformation. See image below. 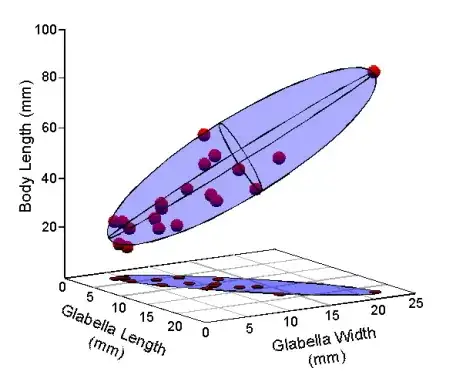enter image description here

The part that is unclear is that after you standardize your variables, the ellipsoid becomes a ball. All the orthogonal axis have the same length. What is the point of doing PCA then?

denizen of the north
  • 848
  • 1
  • 8
  • 15
  • You are mistaken: after standardization, the ellipsoid is almost never a ball. Consider the 2D case, for instance: the ellipsoid in standardized coordinates is always inscribed in a square and thus is oriented at 45 degrees to the axes. – whuber Feb 05 '20 at 15:27
  • 1
    @whuber Exactly what I am looking for. Problem solved. – denizen of the north Feb 05 '20 at 15:48

0 Answers0