I've drawn the following DAG to represent my data generating process
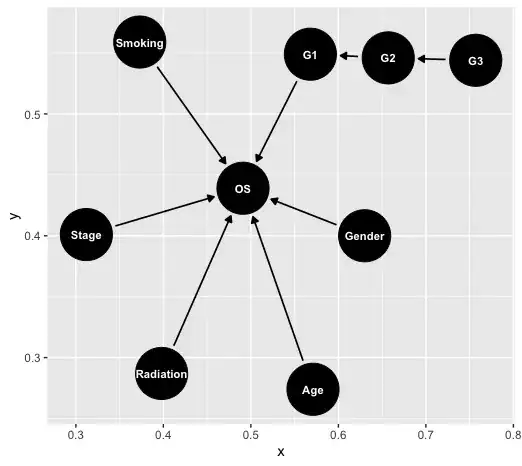
I'm interested in estimating the effects of G1 and G3 on OS via a linear model. It's my understanding that assuming the DAG is correct, I can estimate the effect of G1 by conditioning on G1 alone because it's directly related to OS. To estimate G3, I should avoid conditioning on G2 because it's a mediator. I could use the following model forms:
$$Y = \beta_{G1}X_{G1}$$
$$Y = \beta_{G3}X_{G3}$$
My question regards conditioning on the other, non-mediator variables that affect OS. Should I include Smoking, Stage, Gender, Age, and Radiation in the models? They don't seem to meet the definition of confounder from this post, but I wasn't sure if including these variables could yield more accurate estimates (assuming I have sufficient samples).
Should non-confounders that still affect the outcome be included in regression models to increase precision?