Problems with mixed model simulation

Question

So i was just having a nice evening trying to simulate some hierarchical models by myself and estimate their parameters. First model I tried to simulate and estimate was $$y_{ij}=\beta_0+\varepsilon_{ij},$$ where $b_0=\gamma_{00}+u_{0j}$. So actually what I was estimating was $y_{ij}=\gamma_{00}+u_{0j}+\varepsilon_{ij}$. I have generated some data and estimated parameters $\gamma_{00}$ and variances of error terms and everything was fine:

set.seed(1)
N <- 100
nj <- 100
g00 <- 10
e <- rnorm(N*nj)
j <- c(sapply(1:N, function(x) rep(x, nj)))
uj <- c(sapply(1:N, function(x)rep(rnorm(1), nj)))
d <- data.frame(j, y=g00+uj+e)
library(nlme)
lme(y~1, data=d, random=~1|j)

Linear mixed-effects model fit by REML
  Data: d 
  Log-restricted-likelihood: -14520.94
  Fixed: y ~ 1 
(Intercept) 
   10.00215 

Random effects:
 Formula: ~1 | j
        (Intercept) Residual
StdDev:   0.7752422 1.012683

Number of Observations: 10000
Number of Groups: 100 

Then I tried different model: $$y_{ij}=\beta_0+\beta_1 x_{ij}+\varepsilon_{ij},$$ where $\beta_0=\gamma_{00}+u_{0j}$ and $\beta_1=\gamma_{10}+u_{1j}$. So I had to estimate the equation $$y_{ij}=\gamma_{00}+u_{0j}+(\gamma_{10}+u_{1j}) \cdot x_{ij}+\varepsilon_{ij}=\gamma_{00}+\gamma_{10}x_ij+u_{0j}+u_{1j}x_{ij}+\varepsilon_{ij}.$$ I did the same thing that I had before, but this time lme did not converge. I tried this, but it didn't seem to work.

g10 <- 10
u0j <- uj
u1j <- c(sapply(1:N, function(x)rep(rnorm(1), nj)))
x1 <- rnorm(N*nj)
d1 <- data.frame(j, y=g00+u0j+(g10+u1j)*x1, x1)
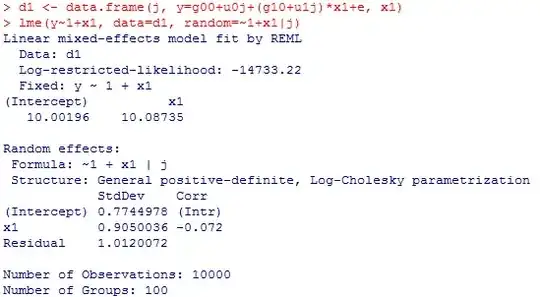
lme(y~1+x1, data=d1, random=~1+x1|j)

Here is what last call to lme spit out:

Error in lme.formula(y ~ 1 + x1, data = d1, random = ~1 + x1 | j) : 
  nlminb problem, convergence error code = 1
  message = false convergence (8)

What can you suggest me to do? Maybe the problem is with my model specification, redundant parameters, singular matrix or something else?

Answer 1

As ?lmeControl says, the default optimizer function is nlminb rather than optim. ?nlminb, however, says that optim is preferred and, indeed, the following works.

lme(y~1+x1, data=d1, random=~1+x1|j, control = lmeControl(opt = "optim"))
Linear mixed-effects model fit by REML
  Data: d1 
  Log-restricted-likelihood: 320824.3
  Fixed: y ~ 1 + x1 
(Intercept)          x1 
   8.302459    8.183053 

Random effects:
 Formula: ~1 + x1 | j
 Structure: General positive-definite, Log-Cholesky parametrization
            StdDev       Corr  
(Intercept) 1.699207e+00 (Intr)
x1          1.952189e+00 0.752 
Residual    1.347943e-15       

Number of Observations: 10000
Number of Groups: 100 

It's hard to say why exactly that's the case. In general, one can see that false convergence (8) means

the gradient $\nabla f(x)$ may be computed incorrectly, the other stopping tolerances may be too tight, or either $f$ or $\nabla f$ may be discontinuous near the current iterate $x$

Answer 2

d1 <- data.frame(j, y=g00+u0j+(g10+u1j)*x1+e, x1) # You need to add error terms

My intuition is that when we simulatated a mixed model data set without error terms, sometimes it may be difficult to converge. This is likely to be a zero residual problem.

Answer 3

This works for me. Instead of using nlme or lmer, I use mgcv::gamm and specify a gaussian link as follows:

GAMM(y~1+x1, data=d1, random=~1+x1|j,family = gaussian)

The estimation results are close to nlme/lmer mixed models and is applicable for most of the cases. In fact, the HLM/mixed model is a specific case of GAMM.

Answer 4

I might be missing a simpler answer (i.e., mis-specification in your model), but /if/ I was sure that the mixed model should converge, I would move on to using openbugs, which will let you drag out a much longer mcmc sample.