3 points are randomly selected from a multinormal distribution $\mathcal{N}(\vec{0},\Sigma)$ in $\mathbb{R^3}$ with $\Sigma=\begin{pmatrix}\sigma^2&0 &0 \\0&\sigma^2&0\\0&0&\sigma^2 \end{pmatrix}$ and variance $\sigma^2$.
How to prove that the expected absolute triangle area of the 3 random points is presumably $\mathbb{E}(A)=\sqrt{3}\sigma^2$? The conjecture was found by simulations.
Rather than an answer I want to extend your speculation: The distribution of the area with $\sigma=1$ has a Gamma distribution with parameters 2 and $\sqrt{3}/2$.
Why? First, a histogram of random samples looks very much like a Gamma distribution. (I'm using Mathematica here because I know the OP also uses Mathematica.)
(* Define the area of the triangle of 3 points in 3-space *)
x1 = {x[1], x[2], x[3]};
x2 = {x[4], x[5], x[6]};
x3 = {x[7], x[8], x[9]};
area = Area[Polygon[{x1, x2, x3}]]
$$\frac{1}{2} \sqrt{(x_2 (x_4-x_7)+x_5 x_7-x_4 x_8+x1 (x_8-x_5))^2+(x_3 (x_4-x_7)+x_6 x_7-x_4 x_9+x_1 (x_9-x_6))^2+(x_3 (x_5-x_8)+x_6 x_8-x_5 x_9+x_2 (x_9-x_6))^2}$$
(* Look at the distribution of some random samples of area *)
n = 10000;
a = ConstantArray[0, n];
Do[a[[j]] = area /. Thread[Table[x[i], {i, 9}] ->
RandomVariate[NormalDistribution[0, 1], 9]], {j, n}]
Histogram[a, Automatic, "PDF"]
Fortunately all of the even moments of the random variable area are readily determined. So we'll match the 2nd and 4th moments of area with that of a Gamma distribution and determine the parameters of the Gamma distribution.
(* Expectation of 2nd and 4th moments of area *)
m2 = Expectation[area^2, Table[x[i] \[Distributed] NormalDistribution[0, 1], {i, 9}]]
(* 9/2 *)
m4 = Expectation[area^4, Table[x[i] \[Distributed] NormalDistribution[0, 1], {i, 9}]]
(* 135/2 *)
(* Expectation of 2nd and 4th moments of a gamma distribution *)
g2 = Expectation[z^2, z \[Distributed] GammaDistribution[a, b]]
(* a (1+a) b^2 *)
g4 = Expectation[z^4, z \[Distributed] GammaDistribution[a, b]]
(* a (1+a) (2+a) (3+a) b^4 *)
(* Get solution(s) for a and b where a > 0 and b > 0 *)
Select[{a, b} /. Solve[{m2 == g2, m4 == g4}, {a, b}], #[[1]] > 0 && #[[2]] > 0 &][[1]]
(* {2,Sqrt[3]/2} *)
So we have a Gamma distribution with parameters $2$ and $\sqrt{3}/2$ which has a mean of $2 \times \sqrt{3}/2=\sqrt{3}$.
But do higher order moments now match? Yes.
TableForm[
Table[{2 k, Expectation[area^(2 k),
Table[x[i] \[Distributed] NormalDistribution[0, 1], {i, 9}]],
Expectation[z^(2 k), z \[Distributed] GammaDistribution[2, Sqrt[3]/2]]}, {k, 1, 5}],
TableHeadings -> {None, {"\nk", "\nE[area^k]", "k-th moment of a\nGamma(2,3^(1/2)/2)"}}]
It looks like a Gamma and we can match (eventually) many even moments.
This doesn't get you a proof but if the distribution of the area is really a multiple of a Gamma distribution, then that might suggest some avenues to go about getting a proof to others. (This approach will almost certainly apply to your cross-product questions on several of these forums.)
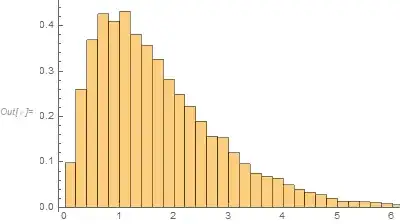
This problem can be solved through a series of simplifications and then looking things up.
First, $\sigma$ merely establishes a unit of measurement: in a system where $\sigma$ is one unit, the covariance matrix is the identity and the unit of area is $\sigma^2:$ that's why the result is a multiple of $\sigma^2.$ So from now on we may take $\sigma=1.$
Second, let the three (independent) random points (each with coordinates from this trivariate standard Normal distribution) be $X,$ $Y,$ and $Z.$ Let $i$ denote one of the three components of these vectors. The triangle in question can be translated to the origin (without changing its area) by subtracting $Z,$ where it is determined by the vectors $U = X-Z$ and $V = Y-Z.$ The components of these vectors are Normal with zero means and covariances
$$\operatorname{Cov}(U_i,V_i) = \operatorname{Cov}(X_i-Z_i, Y_i-Z_i) = 1$$
and variances
$$\operatorname{Var}(V_i) = \operatorname{Var}(U_i) = \operatorname{Var}(X_i-Z_i) = 2.$$
Consequently the correlation of $U_i$ and $V_i$ is $\rho = 1/2.$
Third, we may exploit properties of Normal distributions to describe the distribution of $U,V$ in an equivalent way. Define $\rho^\prime = \sqrt{1-\rho^2}$ so that $\rho^2 + (\rho^\prime)^2 = 1.$
An equivalent description of the distribution of $(U,V)$ begins with independent components $U_i,W_i$ (all with zero mean and variance of $2.$) If we set
$$V = \rho^\prime\,W + \rho\,U$$
then
$$\operatorname{Var}(V) = (\rho^2 + (\rho^\prime)^2)(2) = 2$$
and
$$\operatorname{Cov}(U,V) = \rho\,(2) = 2\rho.$$
This version of $(U,V),$ which (in $n=3$ dimensions) also is $2n$-variate Normal, has exactly the same first and second moments as the original description: thus the distributions are the same.
Fourth, geometry tells us the area of the triangle $OVU$ is the same as the area of the triangle $O(\rho^\prime W)U$ and that, in turn, is $\rho^\prime$ times the area of triangle $OWU,$ which trigonometry tells us is
$$\operatorname{Area}(OWU) = \frac{1}{2} |W|\,|U|\,\sin(\theta_{UW}).$$ Here, $\theta_{UW}$ is the angle made between vectors $U$ and $W.$
Now we may call on well-known (simple) results:
$|U|/\sqrt{2}$ and $|W|/\sqrt{2}$ have $\chi(n)$ distributions.
$t = (1 + \cos(\theta_{UW}))/2$ has a Beta$((n-1)/2, (n-1)/2)$ distribution..
$|U|,|W|,$ and $\theta_{UW}$ are independent. (This follows directly from the spherical symmetry of the $n$-variate standard Normal distribution.)
This information is enough to work out the distribution of the area. (When $n=3$ it happens to have a Gamma distribution but in other dimensions its PDF is proportional to a modified Bessel $K$ function.)
The expected area is particularly easy to find. We can look up (or readily) compute the $\chi(n)$ expectation,
$$E\left[\frac{|U|}{\sqrt{2}}\right] = E\left[\frac{|W|}{\sqrt{2}}\right] = \sqrt{2} \frac{\Gamma((n+1)/2)}{\Gamma(n/2)},$$
and with almost no work we can find the expectation of $\sin(\theta_{UV}) = 2\sqrt{t(1-t)}$ as
$$\eqalign{ E\left[2t^{1/2}(1-t)^{1/2}\right] &= \frac{1}{B((n-1)/2,(n-1)/2)} \int_0^1 2t^{1/2}(1-t)^{1/2} t^{(n-1)/2-1}(1-t)^{(n-1)/2-1}\, \mathrm{d}t \\ &= \frac{2}{B((n-1)/2,(n-1)/2)} \int_0^1 t^{n/2-1}(1-t)^{n/2-1}\, \mathrm{d}t \\ &= \frac{2\,B(n/2,n/2)}{B((n-1)/2,(n-1)/2)}. } $$
Plug everything into the area formula for triangle $OWU$ to obtain
$$\eqalign{ E[\operatorname{Area}(OWU)] &= E\left[\frac{1}{2} |W|\,|U|\,\sin(\theta_{UW})\right] \\ & = \frac{1}{2} \left((\sqrt{2})(\sqrt{2}) \frac{\Gamma\left(\frac{n+1}{2}\right)}{\Gamma\left(\frac{n}{2}\right)}\right)^2\ \frac{2\,B\left(\frac{n}{2},\frac{n}{2}\right)}{B\left(\frac{n-1}{2},\frac{n-1}{2}\right)} \\ & = 4\frac{\Gamma\left(\frac{n+1}{2}\right)^2 \Gamma(n-1)}{\Gamma\left(\frac{n-1}{2}\right)^2 \Gamma(n)} \\ &= 4 \frac{\left(\frac{n-1}{2}\right)^2}{n-1} = n-1. }$$
(The third line expanded the Beta functions in terms of Gamma functions and the last line used the defining relation $\Gamma(z+1) = z\Gamma(z)$ several times.)
We must remember the other two factors dropped along the way: this area has to be multiplied by $\rho^\prime$ (lost at step 4) and then by $\sigma^2$ (lost at step 1).
We have thereby obtained a general formula for the expectation of a triangular area in any number of dimensions and even when the components of the vectors $U$ and $V$ are correlated with correlation coefficient $\rho.$ (Bear in mind these components have variances of $2,$ not $1.$) It is
$$E[\operatorname{Area}(OVU)] = \rho^\prime\, (n-1)\, \sigma^2.$$
Earlier we saw that $\rho=1/2,$ so $\rho^\prime = \sqrt{3}/2$ (there is where the square root of $3$ comes from!) and for $n=3$ this yields
$$E[\operatorname{Area}(XYZ)] = \sqrt{3}\, \sigma^2.$$
