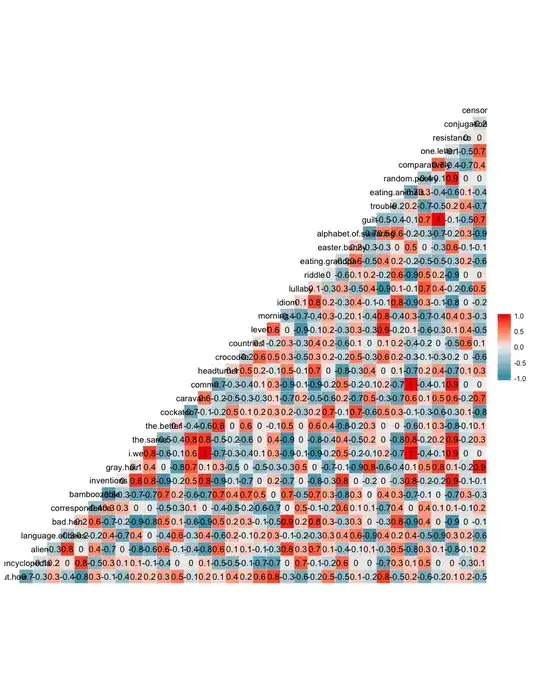
I am using the Wage data set from here. I created a qq plot in R like so: ggqqplot(Wage$age, ylab = "Wage").
The best-fit line starts below zero, which for me is strange. I would expect it to start with the lowest age that exists in the data set (in this case it is 18).
If I instead generate some random numbers that follow the normal distribution: numbers <- rtnorm(3000, 50, 3, 10, 100) the lowest value I have is then 39. If I plot this the best-fit line starts at 39, which I would expect.
I feel like I am missing something obvious here, but can't really understand what.