I'm using a time-series model to do weekly forecasts on the number of incoming calls to a company. This variable has a weekly 'in-month' pattern and a monthly 'in year' pattern, and i have data from 2008-01-01 to 2012-08-31.
To explain it better: Mondays show peaks along weeks, and rainy months show peaks along the year.
My idea is to take the week-forecast point and 'distribute' it along the week days, using the weekly-pattern information.
What is a good technique to do this? Empirical density distributions maybe? My tools: R language.
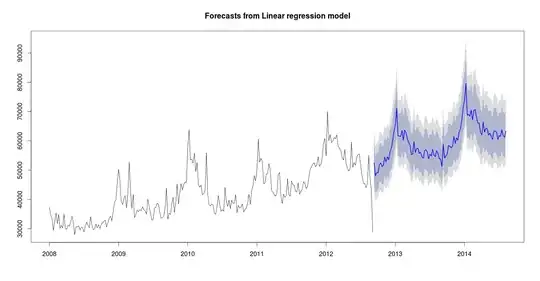
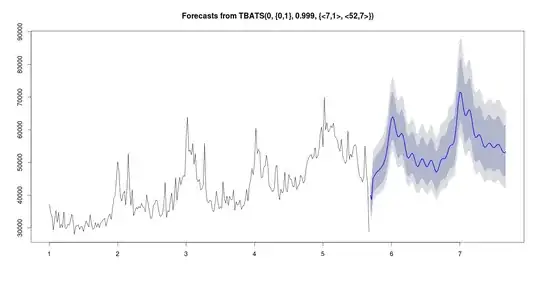
Edit: Below, weekly forecasts using 2 different methods.
Results from tbats using the forecast package:
Results from tslm using the forecast package: