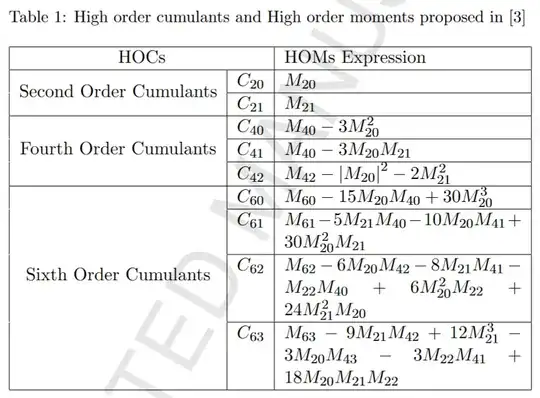
I want to calculate higher-order joint cumulants for 2 variables. I calculated the higher order single-variable and bivariate moments numerically. Now I need to combine them into cumulants (upto the 6th order cumulant, eg k_{3,3})
However, surprisingly, I was unable to find the equations for this anywhere online. Wikipedia (see link above) gives the general formula and provides a few examples for joint cumulants. Also, the summary wolfram site gives a few more examples for bivariate cumulants. However, I was not able to find any comprehensive table that gives all the equations. I feel I understand the formula and the partition concept, but it is tedious to do all the calculations by hand and I dont trust myself not to make an error.
My questions are:
1) Do these equations exist anywhere online?
2) Is there an easy way to get these equations using computing software like Python or Matlab?
3) If not, what else can I do to get them?
Thanks!